filmov
tv
Definition :- Quotient Space

Показать описание
Hello friends, In this video we see the definition of Quotient Space.
Let N be a any vector space and M is subspace then Quotient Space N/M is defined as collection of all left cosets
N/M = { x+M/ x is in N}.
and this N/M (Quotient Space ) is Vector space. with binary operations
for x+M and y+M are in N/M and a in F
I) (x+M) + (y+M)= (x+y)+M
II) a(x+M) = ax+M
with zero element as M
and one thing is to be noted that
if x is in N and also this x is in M. then the left coset formed by this x is same as M
i.e. x is M then x+M = M ( proof is in video)
Quotient Space is normed linear space
Quotient Space is Banach space
#quotientspace
#vectorspace
#functionalanalysis
#banachspace
#normedlinearspace
#subspace
Quotient Space hindi
what is Quotient Space in functional analysis
what is Quotient Space in Banach space
Quotient Space definition
examples of Quotient Space
Quotient Space is Vector space
Let N be a any vector space and M is subspace then Quotient Space N/M is defined as collection of all left cosets
N/M = { x+M/ x is in N}.
and this N/M (Quotient Space ) is Vector space. with binary operations
for x+M and y+M are in N/M and a in F
I) (x+M) + (y+M)= (x+y)+M
II) a(x+M) = ax+M
with zero element as M
and one thing is to be noted that
if x is in N and also this x is in M. then the left coset formed by this x is same as M
i.e. x is M then x+M = M ( proof is in video)
Quotient Space is normed linear space
Quotient Space is Banach space
#quotientspace
#vectorspace
#functionalanalysis
#banachspace
#normedlinearspace
#subspace
Quotient Space hindi
what is Quotient Space in functional analysis
what is Quotient Space in Banach space
Quotient Space definition
examples of Quotient Space
Quotient Space is Vector space
Definition :- Quotient Space
What is...a quotient vector space?
Sphere as the quotient space of a disk
Quotient Space - Definition - Linear Algebra - lesson 19
(Lecture 19) Quotient Vector Spaces
Quotients of Vector Spaces
Abstract vector spaces | Chapter 16, Essence of linear algebra
Definition of a quotient space | QUOTIENT SPACE |TYBSC | MU
Harmonic Analysis and Banach Algebras. Lecture 10. A. Pirkovskii
Quotient Space
Lecture - 5.3 Quotient Spaces
Quotient Space||Definition With Example||Odia Explanation ||B.sc/Msc Math #odia #ugmaths #csirnet
Advanced Linear Algebra, Lecture 1.4: Quotient spaces
The formal definition of a quotient space
Quotient Space || Definition || Theorem In Urdu/ Hindi
Linear Algebra review: Quotient Spaces
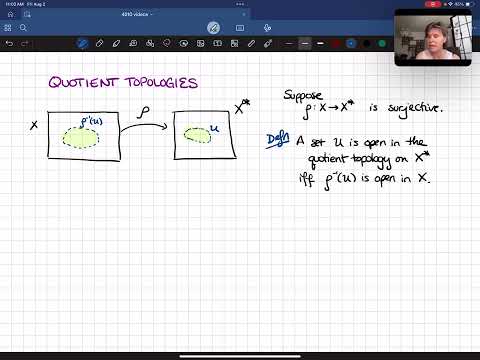
Quotient topology
Quotient Space (+ Pics, Properties & Proofs)
Topology Lecture 14: Quotient Spaces I
Quotient space (linear algebra) | Wikipedia audio article
The following exercise requires familiarity with the definition of quotient space given in Exercise…...
Quotient Space is vector space and operation are well defined proof
Chapter 5: Quotient groups | Essence of Group Theory
Quotient space (topology)
Комментарии
 0:08:33
0:08:33
 0:12:22
0:12:22
 0:00:33
0:00:33
 0:06:46
0:06:46
 0:52:02
0:52:02
 0:09:07
0:09:07
 0:16:46
0:16:46
 0:05:22
0:05:22
 1:12:38
1:12:38
 0:12:44
0:12:44
 0:40:56
0:40:56
 0:17:15
0:17:15
 0:43:57
0:43:57
 0:01:40
0:01:40
 0:20:52
0:20:52
 0:08:53
0:08:53
 0:03:29
0:03:29
 0:19:27
0:19:27
 1:00:58
1:00:58
 0:09:35
0:09:35
 0:00:33
0:00:33
 0:16:46
0:16:46
 0:12:37
0:12:37
 0:06:33
0:06:33