filmov
tv
Circle Theorem Theorems Alternate Segment Opposite Angles Cyclic Quadrilateral Triangle Isosceles
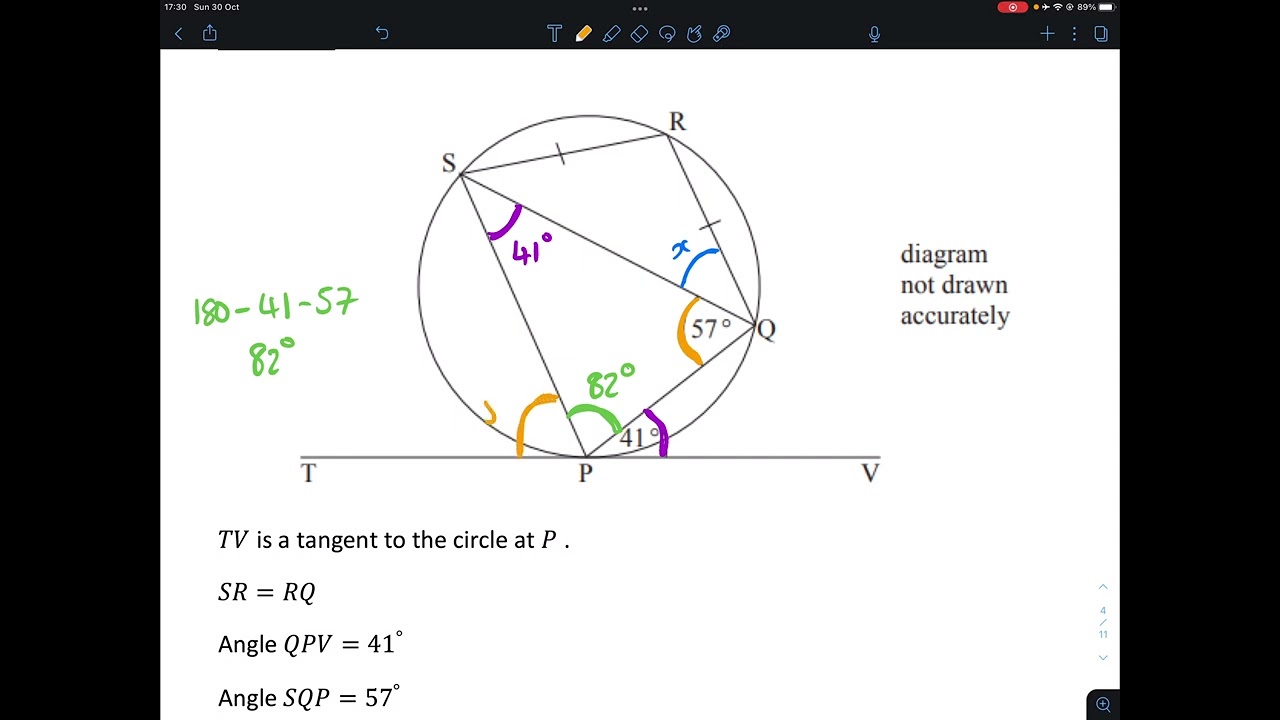
Показать описание
Understand Alternate Segment Theorem to find equal angles in Circle | ACT SAT | GCSE Maths
GCSE (9 - 1) Maths - Circle Theorems - Lesson 7:Alternate Segment Theorem
Key Skill - Alternate Segment Theorem
Alternate segment theorem animation
Circle Theorems: Alternate Segment Theorem (Grade 7) - OnMaths GCSE Maths Revision
Circle theorems and the Alternate Segment Theorem made easy - (Maths GCSE Revision)
Circle Theorems - GCSE Higher Maths
Everything About Circle Theorems - In 3 minutes!
Circle Theorems, alternate segment theorem and simultaneous equations
IGCSE Circle Theorems: My Best A* Tip...
Circle Theorem 8 Proof - Alternate Segment Theorem # #circletheorem #mathinar
What is the Alternate Segment Theorem | Circle Theorems
Circle Theorem | Alternate circle theorem.
Circle Theorem Theorems Alternate Segment Opposite Angles Cyclic Quadrilateral Triangle Isosceles
Circle theorems alternate segment theorem
Circle Theorem Alternate Segment and Chord Theorem Proof and Exam Preparation | GCSE | SAT ACT
Circle Theorem Exam Question - Alternate Segment
Alternate segment theorem of Circle!! Important from SSC -CGL point of view #shorts#youtube
Maths circle theorems Alternate segment theorem
GCSE Maths revision Exam practice circle theorems - Alternate segment theorem & Cyclic quad
Understanding Alternate Segment Theorem.
ALTERNATE SEGMENT.CIRCLE THEOREM
Circle Theorems: the alternate segment theorem example
Circle Theorems!
Комментарии
 0:05:30
0:05:30
 0:02:44
0:02:44
 0:03:42
0:03:42
 0:00:20
0:00:20
 0:02:04
0:02:04
 0:02:36
0:02:36
 0:13:53
0:13:53
 0:04:11
0:04:11
 0:02:13
0:02:13
 0:00:19
0:00:19
 0:01:01
0:01:01
 0:02:39
0:02:39
 0:01:00
0:01:00
 0:03:49
0:03:49
 0:01:51
0:01:51
 0:33:01
0:33:01
 0:04:38
0:04:38
 0:00:55
0:00:55
 0:00:48
0:00:48
 0:06:31
0:06:31
 0:08:04
0:08:04
 0:01:01
0:01:01
 0:02:43
0:02:43
 0:00:16
0:00:16