filmov
tv
Emergence of Chaos in Damped-Driven Nonlinear Pendulum
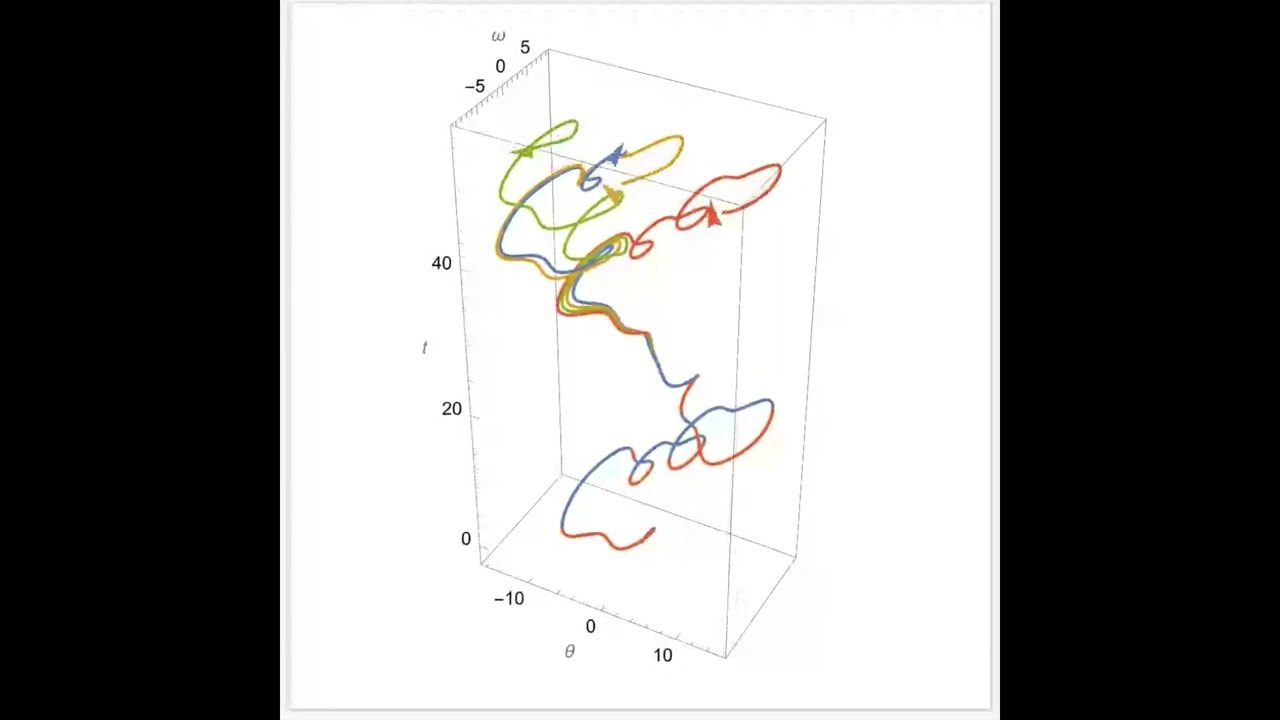
Показать описание
This animation was made in Mathematica and it shows the deviation in phase trajectory for damped-driven nonlinear pendulums with similar initial conditions ($0.147\leq\theta(0)\leq 0.150$). This demonstrates the Poincaré–Bendixson theorem, showing that chaos emerges when the phase space is 3-dimensional and there is at least 1 nonlinear coupling. Here $t$ is the time elapsed, $\theta$ is the angular displacement, and $\omega$ is the angular velocity.
 0:00:26
0:00:26
 0:00:27
0:00:27
 0:00:40
0:00:40
 0:02:38
0:02:38
 0:02:03
0:02:03
 0:00:13
0:00:13
 0:06:48
0:06:48
 0:00:11
0:00:11
 0:13:06
0:13:06
 0:11:40
0:11:40
 0:01:16
0:01:16
 0:01:30
0:01:30
 0:45:48
0:45:48
 0:00:21
0:00:21
 0:29:47
0:29:47
 0:00:11
0:00:11
 0:42:53
0:42:53
 0:04:03
0:04:03
 0:36:57
0:36:57
 0:00:11
0:00:11
 0:01:54
0:01:54
 0:29:36
0:29:36
 0:19:42
0:19:42
 0:27:19
0:27:19