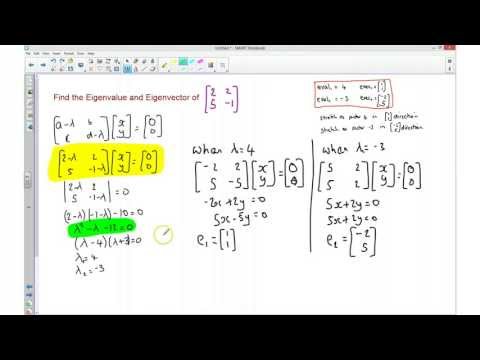
AQA FP4 - Eigenvalues and Eigenvectors 2

preview_player
Показать описание
AQA FP4 - Eigenvalues and Eigenvectors 2
  1. Mohammed Ladak
  2. Screencast-O-Matic.com
Рекомендации по теме
AQA FP4 - 0:28:49

AQA FP4 - Eigenvalues and Eigenvectors 1

AQA FP4 - 0:17:00

AQA FP4 - Eigenvalues and Eigenvectors 4

AQA FP4 - 0:12:42

AQA FP4 - Eigenvalues and Eigenvectors 3

AQA FP4 - 0:10:37

AQA FP4 - Eigenvalues and Eigenvectors 5 (Diagonalisation)

FMSP Revision: AQA 0:16:03

FMSP Revision: AQA FP4 June 2010 qn 7 Eigenvalues and Eigenvectors

AQA FP4 - 0:20:59

AQA FP4 - Eigenvalues and Eigenvectors 2

FMSP Revision: AQA 0:18:31

FMSP Revision: AQA FP4 January 2010 qn 7 Eigenvalues and Eigenvectors

AQA FP4 Jan 0:11:54

AQA FP4 Jan 2013 Q7

AQA FP4 Jan 0:15:15

AQA FP4 Jan 2010 Q4

FMSP Revision: AQA 0:08:13

FMSP Revision: AQA FP4 June 2011 qn 2 Matrices and Transformations

FMSP Revision: AQA 0:13:22

FMSP Revision: AQA FP4 June 2011 qn 6 Matrices and Transformations

AQA FP4 June 0:13:24

AQA FP4 June 2009 Q6

AQA FP4 Jan 0:14:04

AQA FP4 Jan 2013 Q4

AQA FP4 Jan 0:24:12

AQA FP4 Jan 2010 Q7

AQA FP4 Jan 0:06:00

AQA FP4 Jan 2010 Q1

AQA FP4 Jan 0:11:13

AQA FP4 Jan 2013 Q5

AQA FP4 June 0:21:29

AQA FP4 June 2009 Q4

AQA FP4 Jan 0:12:33

AQA FP4 Jan 2013 Q6

AQA FP4 June 0:10:34

AQA FP4 June 2009 Q8

FMSP Revision: AQA 0:03:02

FMSP Revision: AQA FP4 January 2010 qn 1 Matrices and Transformations

AQA FP4 June 0:15:38

AQA FP4 June 2009 Q7

AQA FP4 Jan 0:10:05

AQA FP4 Jan 2010 Q2

FMSP Revision: AQA 0:10:25

FMSP Revision: AQA FP4 January 2010 qn 5 Matrices and Transformations

AQA FP4 Jan 0:12:25

AQA FP4 Jan 2010 Q5

Комментарии
Автор

the eigenvectors and values reveals that there is an enlargement in the direction of a line through the origin. the other eigenvector is the axis the shear is parallel to with an eigenvalue of 1. so guess the resultant is enlargement in the direction corresponding to the eigenvalue that isnt 1.

MrJarastamon
Автор

So the special case of an Eigen value of 1 represents a shear always?
How about if we had a Matrix which have eigen values 1 (eigen vector that is not parallel to the axis) and 2 for example. Would this represent a shear and an enlargement?

MrJarastamon
Автор

What about if I only had a single Eigenvalue of 1? or a single eigenvalue of 2?

mathedup
Автор

Try writing a matrix that represents a shear parallel to the x-axis (to keep it simple) and a matrix that represents a stretch (case 1: parallel to the y-axis. Case 2: Parallel to the x-axis). Combine the transformations of the shear and the stretch in each case. What are the eigenvalues/eigenvectors. Can you explain why? Now try to answer your question..

mathedup