filmov
tv
ERTH/OCN312: ODE's: Linear 1st order, homogeneous cases
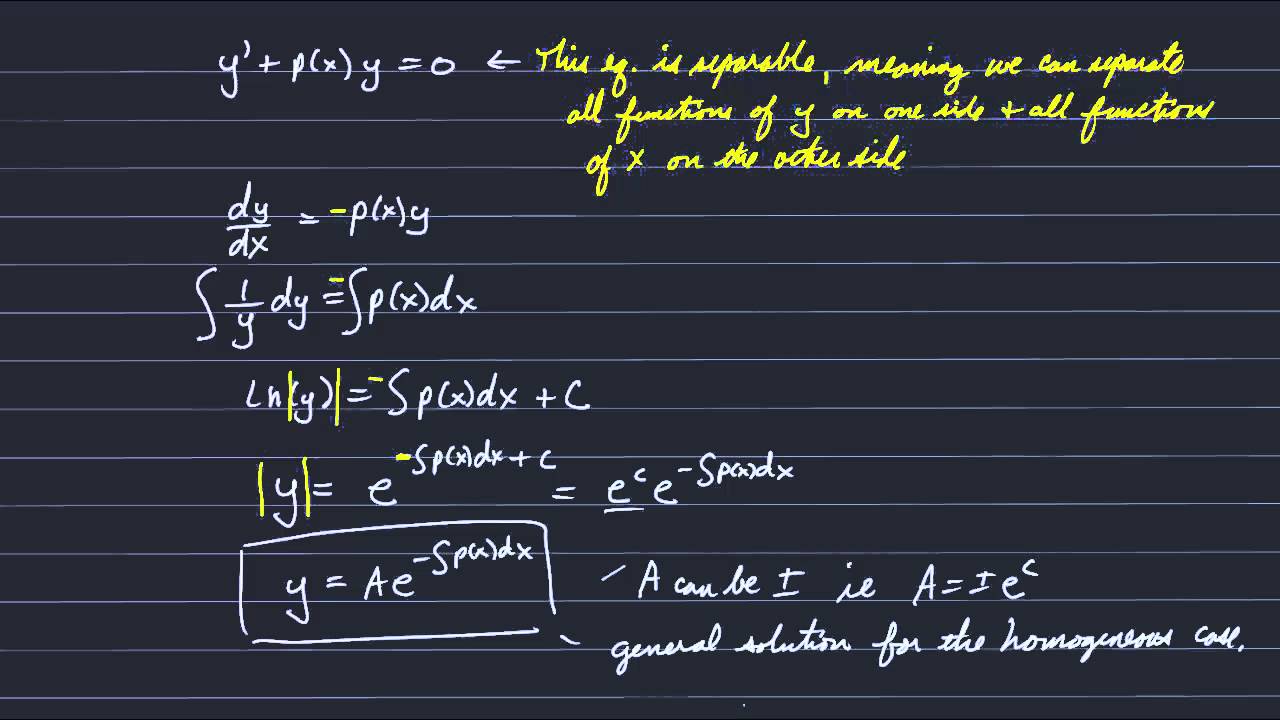
Показать описание
ERTH/OCN312: Advanced Mathematics for Engineers and Scientists
Prof. Garrett Apuzen-Ito
University of Hawaii, Dept. of Earth Sciences
School of Ocean and Earth Science and Technology (SOEST)
Prof. Garrett Apuzen-Ito
University of Hawaii, Dept. of Earth Sciences
School of Ocean and Earth Science and Technology (SOEST)
ERTH/OCN312: ODE's: Linear 1st order, homogeneous cases
ERTH/OCN312 Linear, 1st Order ODE's, Application to Chemical Mixing
ERTH/OCN312: 1st-order, Linear, Non-homogenous ODEs II: Variation of Parameters
ERTH/OCN312: Non-homogeneous Linear ODE: Integrating Factor Method
ERTH/OCN312 General solution to the n-order linear homogeneous ODE
ERTH/OCN312: Separable First Order ODE's
ERTH/OCN 312: Solution to non-linear ODE by method of undetermined coefficients
ERTH/OCN312: Applications of ODEs: The RL Electrical Circuit
ERTH/OCN312: Solutions to the Homogeneous Equation with Constant Coefficients
ERTH/OCN312: 1st Order ODE Applications: Mass on a hill
ERTH/OCN312: Homogeneous ODE with Constant Coefficients
ERTH/OCN312: Applications of ODEs: Chemical Mixing
ERTH/OCN312: Higher Order ODE's with Non-Constant Coefficients
ERTH/OCN312: Higher order, non-homogeneous ODE with constant coefficients: Some preliminaries
ERTH/OCN312: Finding the Integrating Factor that Makes an Exact Differential
ERTH/OCN312 Systems of Linear Equations and Gauss Elimination
OCN/ERTH312: Introduction to Differential Equations
ERTH/OCN312: Applications of ODEs: Radioactive Decay
ERTH/OCN 312: Introduction to Advanced Mathematics
ERTH/OCN312: Numerical Methods, Runge-Kutta
ERTH/OCN312: Applications of the Eigenvalue Problem
ERTH/OCN312: Taylor Series Example
ERTH/OCN 312: Matrix Multiplication
Applications of First Order Differential Equations Exponential Decay Part 1
Комментарии
 0:16:08
0:16:08
 0:09:57
0:09:57
 0:23:54
0:23:54
 0:22:17
0:22:17
 0:28:41
0:28:41
 0:28:46
0:28:46
 0:22:01
0:22:01
 0:27:40
0:27:40
 0:36:06
0:36:06
 0:19:47
0:19:47
 0:40:41
0:40:41
 0:12:46
0:12:46
 0:31:01
0:31:01
 0:11:32
0:11:32
 0:28:14
0:28:14
 0:36:18
0:36:18
 0:32:51
0:32:51
 0:10:47
0:10:47
 0:08:50
0:08:50
 0:26:38
0:26:38
 0:21:23
0:21:23
 0:06:58
0:06:58
 0:17:55
0:17:55
 0:06:32
0:06:32