filmov
tv
Limit of x*tan(1/x) as x approaches Infinity (no L'Hospital's Rule) | Calculus 1 Exercises
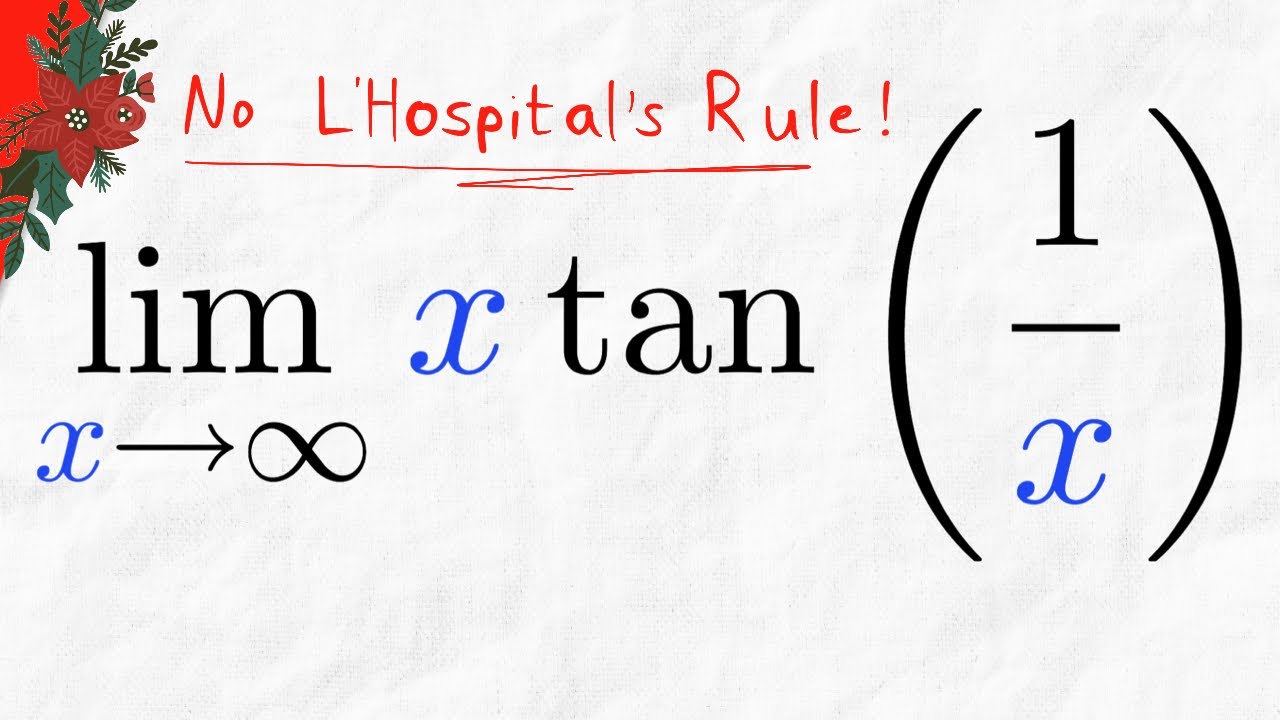
Показать описание
We evaluate the limit of xtan(1/x) as x goes to infinity, which gives us a horizontal asymptote of x*tan(1/x). We'll evaluate this limit without using L'Hospital's rule. Instead, we use the limit product rule, the definition of tangent, the trigonometric limit sin(x)/x as x approaches 0, and then we'll pretty much be done showing that the limit as x approaches infinity of x*tan(1/x) is 1! #Calculus1
Limit of sin(x)/x as x approaches 0: (coming soon)
★DONATE★
Thanks to Robert Rennie, Barbara Sharrock, and Rolf Waefler for their generous support on Patreon!
Follow Wrath of Math on...
Limit of sin(x)/x as x approaches 0: (coming soon)
★DONATE★
Thanks to Robert Rennie, Barbara Sharrock, and Rolf Waefler for their generous support on Patreon!
Follow Wrath of Math on...
limit of x*tan(1/x) as x goes to infinity, L'Hospital's Rule
Limit of x*tan(1/x) as x approaches Infinity (no L'Hospital's Rule) | Calculus 1 Exercises
Calculus 1: Limits & Derivatives (25 of 27) Finding the Limits of a Function - Example 12
Lim tan^-1(x)/x as x tends to 0, # Easy # fast # Short # Trick
Limit of tanx/x as x approaches 0 | Calculus 1 Exercises
Find the limit as x approaches infinity for x tan(1/x). l’Hopital’s Rule
Evaluate the limit as x approaches infinity for (x tan(1/x)). l’Hopital’s Rule
Limit of arctan function as x approaches infinity [Limits at infinity]
Week-9|Doubt session - Maths 1
Evaluate : limit x tends to infinity xtan(1/x)
30 Limit Approaching Infinity for Trigonometric Function xsin(1/x)
Limit of arctanx as x approaches Infinity | Calculus 1 Exercises
limit at infinity arctan(e^x), calculus 1 tutorial
Limits of Trigonometric Functions
Find the limit as x approaches 0 for x/(tan^(-1) (4x)). l’Hopital’s Rule
Limits of Inverse Trigonometric Functions | Calculus
`lim_(x- gtoo)((x+5) tan^-1 (x +5)-(x +1)tan^-1(x+1)` is equal to
Find the limit as x approaches 1^+ for (ln x tan(pi x/2)) l’Hopital’s Rule
lim xsin(1/x) as x goes to 0
1: Lim(x tends to 1 { (1-x) tan(pix/2) has value - l GIC l TGT l PGT l LT l KVS l DSSSB l Calculus
Hitunglah nilai limit dari: limit x mendekati tak hingga (x tan(1/x))
Nilai limit x mendekati tak hingga x(x-1)tan 1/x adalah ....
Limit of (arctan x)/x as x approaches 0
Find the limit as x approaches infinity for sin(tan(1/x)) cot (1/x)
Комментарии
 0:03:36
0:03:36
 0:09:21
0:09:21
 0:01:48
0:01:48
 0:00:16
0:00:16
 0:03:22
0:03:22
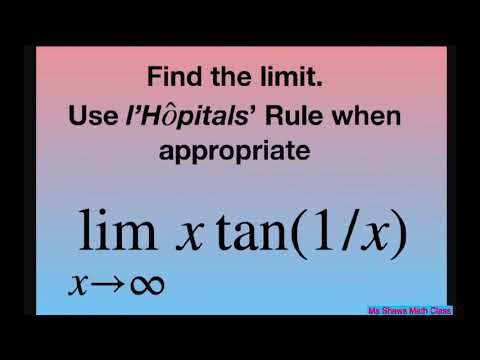 0:02:55
0:02:55
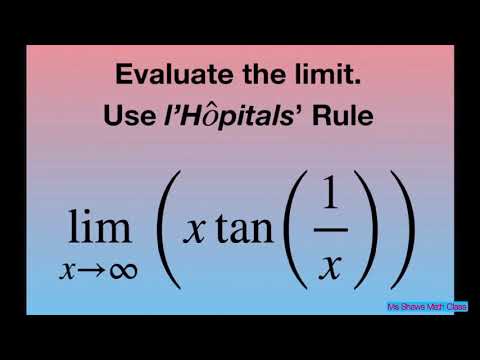 0:02:35
0:02:35
 0:07:09
0:07:09
 2:43:40
2:43:40
 0:03:42
0:03:42
 0:02:24
0:02:24
 0:02:55
0:02:55
 0:02:10
0:02:10
 0:15:23
0:15:23
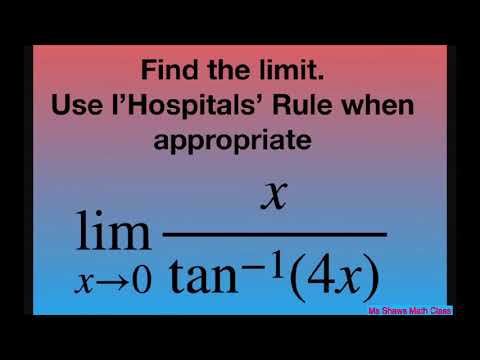 0:02:23
0:02:23
 0:13:17
0:13:17
 0:01:49
0:01:49
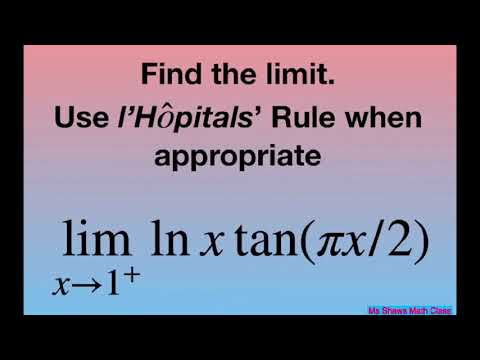 0:02:48
0:02:48
 0:15:35
0:15:35
 0:02:46
0:02:46
 0:02:13
0:02:13
 0:03:00
0:03:00
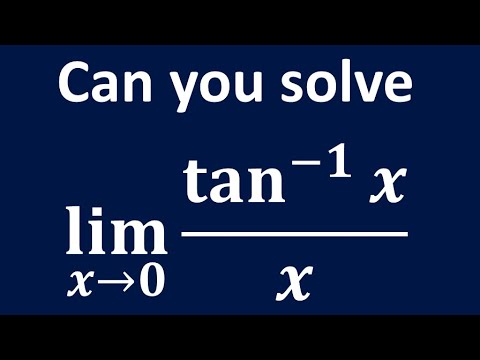 0:03:28
0:03:28
 0:02:52
0:02:52