filmov
tv
Matrix Completion and the Netflix Prize

Показать описание
This video describes how the singular value decomposition (SVD) can be used for matrix completion and recommender systems.
These lectures follow Chapter 1 from: "Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control" by Brunton and Kutz
This video was produced at the University of Washington
These lectures follow Chapter 1 from: "Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control" by Brunton and Kutz
This video was produced at the University of Washington
Matrix Completion and the Netflix Prize
Matrix Completion
Statistical Learning: 12.5 Matrix Completion
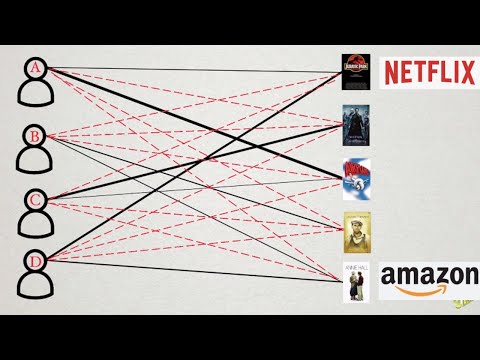
How Recommender Systems Work (Netflix/Amazon)
noc18-ee31 Lecture 79-Matrix Completion Problem in Big Data: Netflix-II
Ankur Moitra, 'Beyond Matrix Completion'
noc18-ee31 Lecture 78-matrix Completion Problem in Big Data: Netflix-I
Lecture27: 3.5 Matrix Completion (Part I). MATH 405: Learning From Data.
Matrix Completion with Nucleus Norm and SVD | Lê Nguyên Hoang
Matrix Completion
Netflix Prize Solution | Recommendation System and Matrix Factorization | EP #13
Image Restoration by Matrix Completion Using Schatten Capped p-Norm
Matrix Completion using the Nuclear Norm for Low Rank Factorization
Inductive Matrix Completion Based on Graph Neural Networks
Introduction to Matrix Completion
NuclearNorm
Causal Matrix Completion
Matrix Factorization in Recommendation Systems | Netflix Recommend Movie
Michael Li - Interpretable Matrix Completion: A Discrete Optimization Approach
Federico Monti: 'Deep Geometric Matrix Completion'
What happened when I fall #surf #surfing #athlete #waves #surfers #skate #wsl #fit
EMBP Algorithm for Matrix Completion
Matrix Completion for the Independence Model
Matrix completion 1/4
Комментарии
 0:06:13
0:06:13
 0:07:57
0:07:57
 0:15:52
0:15:52
 0:08:18
0:08:18
 0:28:20
0:28:20
 0:42:14
0:42:14
 0:24:36
0:24:36
 0:14:25
0:14:25
 0:05:43
0:05:43
 0:16:32
0:16:32
 1:15:49
1:15:49
 0:09:59
0:09:59
 0:07:41
0:07:41
 0:05:14
0:05:14
 0:04:31
0:04:31
 0:01:44
0:01:44
 0:49:50
0:49:50
 0:17:36
0:17:36
 0:10:19
0:10:19
 0:33:37
0:33:37
 0:00:11
0:00:11
 0:13:37
0:13:37
 0:25:26
0:25:26
 0:08:01
0:08:01