filmov
tv
Abstract Algebra: practice problems 9-6-16, chapter 2 and 3 Gallian
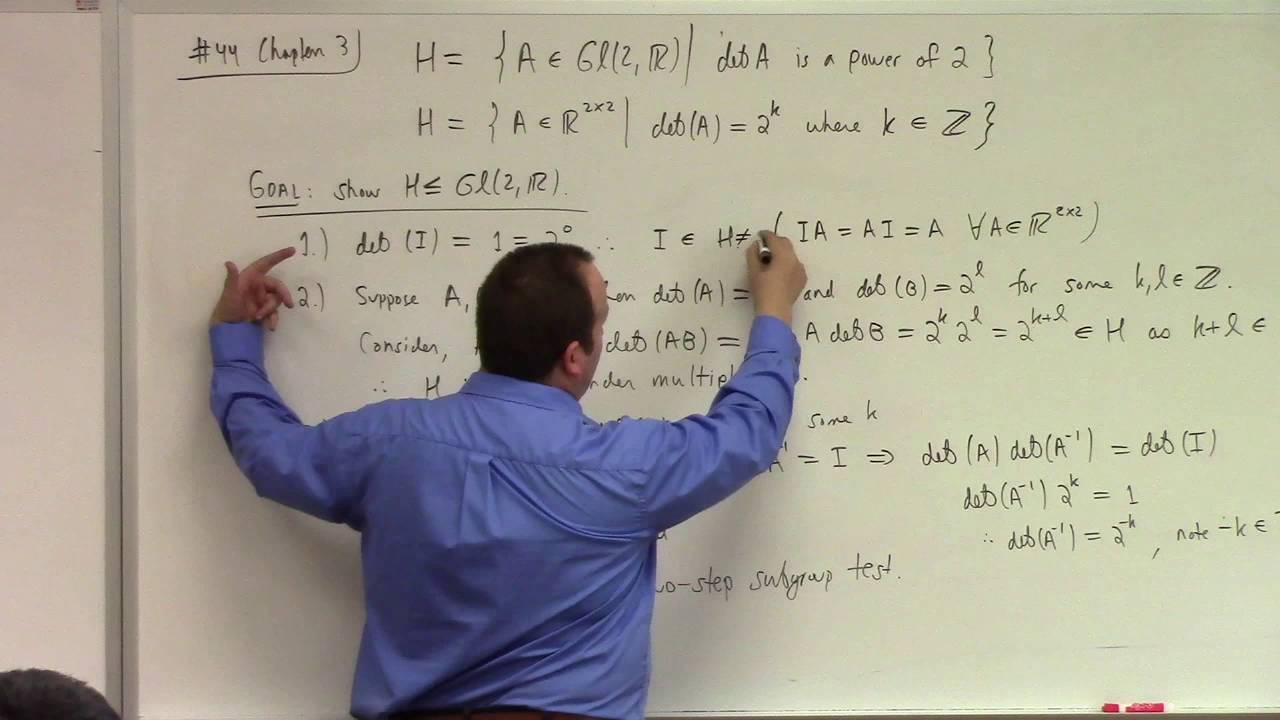
Показать описание
here I work a subgroup test problem and I give the proof that frf=r^(-1) in the case Dn has even n. The proof I gave in Lecture held for odd n. I also answer a few random questions and show U(20) is not cyclic.
Abstract Algebra: practice problems 9-6-16, chapter 2 and 3 Gallian
Abstract Algebra: practice problems 9-8-16, chapter 3 Gallian
Abstract Algebra: practice problems 9-13-16, chapter 4 Gallian
Abstract Algebra: practice problems 9-15-16, chapter 5 Gallian
Abstract Algebra: L6, cyclic groups part 1, 9-9-16
Most💯 Important Step Before any Procedure 🔥
How to Answer Any Question on a Test
BEST DEFENCE ACADEMY IN DEHRADUN | NDA FOUNDATION COURSE AFTER 10TH | NDA COACHING #shorts #nda #ssb
Complex Analysis And Abstract Algebra | CSIR NET Mathematics Dec. 2024 | IFAS Maths | Lecture 10
Can you calculate like shakuntala Devi ?|Human calculator|Shakuntala Devi|India's World record ...
Abstract Algebra: practice problems, chapter 2 and 3 Gallian, 9-1-16
5 simple unsolvable equations
Abstract Algebra: help session, questions, part of Lecture 6, 9-7-18
Abstract Algebra: help session, solutions to Lecture 10,11 and 12 problems, 10-18-16
Abstract Algebra: L5, modular arithmetic foundations, 9-7-16
Aspirants practicing eatingetiquette # SSB #SSBPreparation #NDA #CDS #Defence #DefenceAcademy
Abstract Algebra: help session, 9-29-16
#simplification #tricks
(Abstract Algebra 1) Definition of a Cyclic Group
Logical Reasoning???#viral #vidumzn
Students in first year.. 😂 | #shorts #jennyslectures #jayantikhatrilamba
Shradha didi at lpu 🤩 #apna college #viralshorts
Abstract Algebra: help session, 9-27-16
How to Align Your Navel Correctly With Yogacharya Dhakaram
Комментарии
 0:41:46
0:41:46
 0:46:49
0:46:49
 0:54:35
0:54:35
 0:42:36
0:42:36
 0:51:34
0:51:34
 0:00:16
0:00:16
 0:00:27
0:00:27
 0:00:15
0:00:15
 0:56:30
0:56:30
 0:00:34
0:00:34
 0:44:26
0:44:26
 0:00:50
0:00:50
 0:55:35
0:55:35
 0:55:54
0:55:54
 0:52:18
0:52:18
 0:00:11
0:00:11
 0:47:10
0:47:10
 0:00:11
0:00:11
 0:09:01
0:09:01
 0:00:11
0:00:11
 0:00:11
0:00:11
 0:00:16
0:00:16
 0:45:52
0:45:52
 0:00:40
0:00:40