filmov
tv
Катеты прямоугольного треугольника равны 3 и 4. Найдите высоту, проведённую к гипотенузе

Показать описание
Катеты прямоугольного треугольника равны 3 и 4. Найдите высоту, проведённую к гипотенузе...
Геометрия Катеты прямоугольного треугольника равны 3√91 и 9. Найдите синус наименьшего угла этого...
Катеты прямоугольного треугольника равны 20 и 15. ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРА...
Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математике...
катеты прямоугольного треугольника равны 18 и 24.Найдите длину высоты, проведенной к гипотенузе...
Теорема Пифагора для чайников)))
№4. Катеты прямоугольного треугольника равны 15 и 20. Найдите высоту, проведённую к гипотенузе....
Площадь прямоугольного треугольника равна 180,5∙√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРА...
Реальный вариант ОГЭ 2024 по математике. Задачи 1-19
Площадь прямоугольного треугольника равна (2888√3)/3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРА...
Геометрия Найдите гипотенузу прямоугольного треугольника, если его катеты равны: 1) 3 см и 4 см...
№575. Катеты прямоугольного треугольника относятся как 3 : 4, а гипотенуза равна 50 мм....
Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?...
Лайфхак нахождения катета в прямоугольном треугольнике...
Геометрия Найдите катеты прямоугольного равнобедренного треугольника, гипотенуза которого равна c...
Катеты и гипотенуза
№597. Катеты прямоугольного треугольника равны а и b. Выразите через а и b гипотенузу...
КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрия...
Найдите площадь треугольника, если его медианы равны 3, 4 и 5...
№273. Сумма гипотенузы СЕ и катета CD прямоугольного треугольника CDE равна 31 см, а их...
Геометрия Катет и гипотенуза прямоугольного треугольника равны 15 и 25. Найдите высоту, проведённую...
Свойства прямоугольного треугольника. 7 класс.
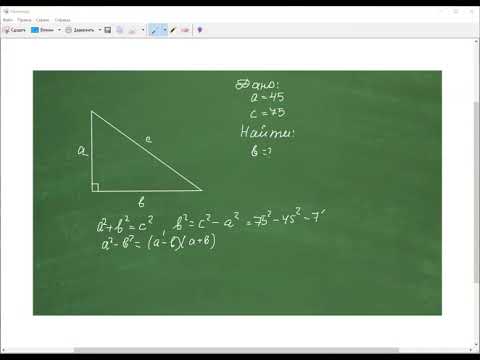
№5. Катет и гипотенуза прямоугольного треугольника равны 21 и 75. Найдите высоту, проведённую к гипо...
Геометрия Катет прямоугольного треугольника равен 48 см, а тангенс противолежащего угла равен 3 3/7...
Комментарии
 0:01:57
0:01:57
 0:02:10
0:02:10
 0:03:18
0:03:18
 0:01:44
0:01:44
 0:03:20
0:03:20
 0:02:04
0:02:04
 0:03:51
0:03:51
 0:03:49
0:03:49
 1:27:08
1:27:08
 0:04:24
0:04:24
 0:02:40
0:02:40
 0:04:03
0:04:03
 0:06:49
0:06:49
 0:01:42
0:01:42
 0:02:26
0:02:26
 0:01:38
0:01:38
 0:03:28
0:03:28
 0:00:42
0:00:42
 0:04:09
0:04:09
 0:01:49
0:01:49
 0:02:55
0:02:55
 0:09:02
0:09:02
 0:03:21
0:03:21
 0:03:15
0:03:15