filmov
tv
A Groundbreaking Mathematical Result
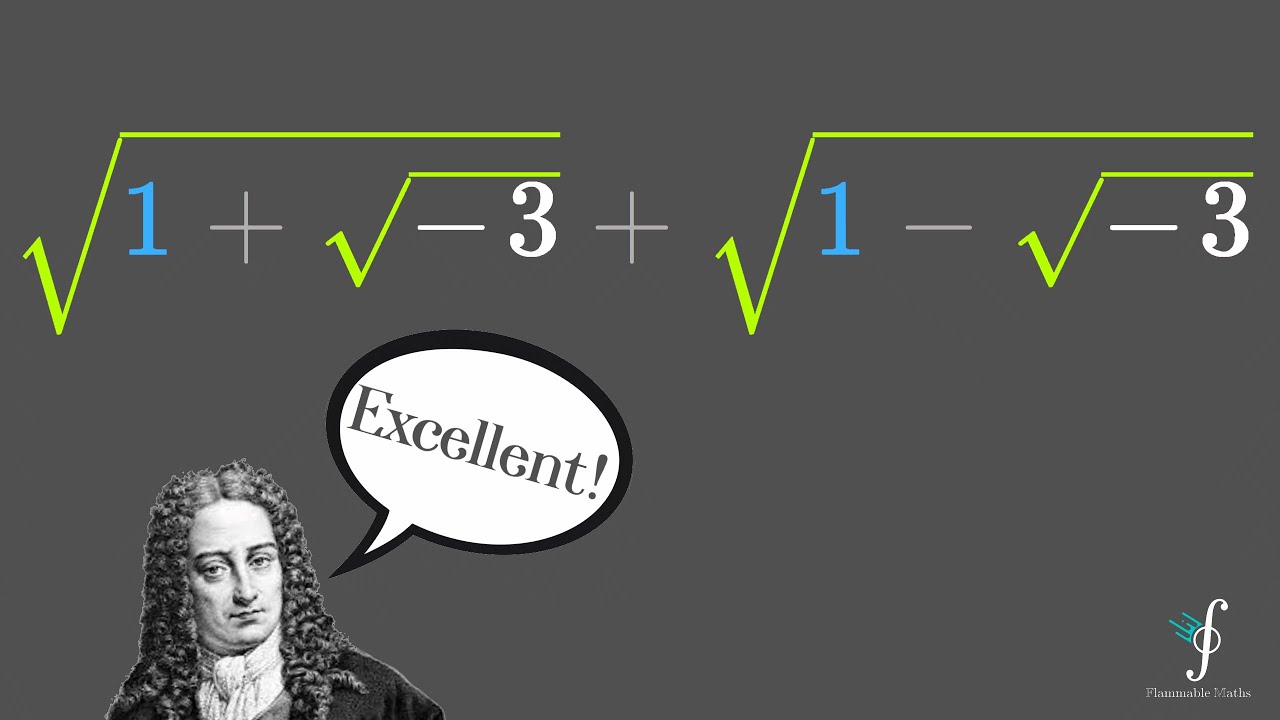
Показать описание
Subscribe to @RockHardWoodDaddy to see your dad working his wood :^D
Thanks Leibniz, very cool! Without complex numbers or the notion of negative arguments in roots, Leibniz shook the mathematical community back in the days by denesting radicals! We are going to explore his result for sqrt(1+sqrt(-3))+sqrt(1-sqrt(-3)) giving us sqrt(6). As a corrolary using the conjugate and difference of two squares, we also find out the value for sqrt(1+sqrt(-3))-sqrt(1-sqrt(-3)) in the process. Enjoy! =)
Help me create more free content! =)
--------------------------------------------------------------------------------
Wanna send me some stuff? lel:
Postfach 11 15
06731 Bitterfeld-Wolfen
Saxony-Anhalt
Germany
--------------------------------------------------------------------------------
Thanks Leibniz, very cool! Without complex numbers or the notion of negative arguments in roots, Leibniz shook the mathematical community back in the days by denesting radicals! We are going to explore his result for sqrt(1+sqrt(-3))+sqrt(1-sqrt(-3)) giving us sqrt(6). As a corrolary using the conjugate and difference of two squares, we also find out the value for sqrt(1+sqrt(-3))-sqrt(1-sqrt(-3)) in the process. Enjoy! =)
Help me create more free content! =)
--------------------------------------------------------------------------------
Wanna send me some stuff? lel:
Postfach 11 15
06731 Bitterfeld-Wolfen
Saxony-Anhalt
Germany
--------------------------------------------------------------------------------
A Groundbreaking Mathematical Result
2023's Biggest Breakthroughs in Math
How Grigori Perelman Solved the 100-Year-Old Math Problem and Changed Topology Forever
Groundbreaking Math Discovery From The 1700s w/ Neil DeGrasse Tyson
Ed Witten’s Quantum Field Theory: More Than Just Math
🧩 Fermat’s Last Theorem: The Greatest Math Mystery Solved! 🔍✨ #MindBlown #MathGenius #MysterySolved...
David Hilbert: The Man Behind Mathematical Rigor #mathematics
Unlocking the Power of Perelman's Revolutionary Math Solution
The Fascinating Journey of Zero: From Nothing to Everything! #zero #mathematics #funfacts #history
The Strangest Mathematician in History
Signa math teacher, Mr. Bean #sigma #math #techera #formula
2020's Biggest Breakthroughs in Math and Computer Science
Part 1 - The man who solve the 1 million usd math problem
Math method with Mr.Bean #techera #math #sigma #math #formula
Revolutionary Ancient Chinese Math Innovations
Did Einstein Really Fail Math? The Truth Uncovered!
The Short Life of a Mathematical Prodigy
The Latte Art That Solved a 200-Year-Old Math Problem
Unlocking Math Mastery: The Groundbreaking Method That Boosted Students' Scores
Srinivasa Ramanujan: The Self-Taught Mathematical Genius
Mathematician Luke Durant Discovered The New Largest Known Prime Number Ever #maths #mathematics
Emmy Noether: The Enigma of Mathematical History
Roger Penrose: The Elegance of Mathematical Simplicity
☠️ Kid Cracks Math Code: 0/0=2 : 'Bro is smarter than Einestien and Nikola tesla'
Комментарии
 0:12:54
0:12:54
 0:19:12
0:19:12
 0:00:49
0:00:49
 0:00:27
0:00:27
 0:00:40
0:00:40
 0:01:05
0:01:05
 0:00:24
0:00:24
 0:00:36
0:00:36
 0:00:59
0:00:59
 0:10:48
0:10:48
 0:00:32
0:00:32
 0:07:46
0:07:46
 0:01:00
0:01:00
 0:00:19
0:00:19
 0:00:45
0:00:45
 0:00:54
0:00:54
 0:00:58
0:00:58
 0:00:16
0:00:16
 0:00:37
0:00:37
 0:00:34
0:00:34
 0:00:06
0:00:06
 0:00:39
0:00:39
 0:00:14
0:00:14
 0:00:08
0:00:08