filmov
tv
Elementary Counting Principles [Discrete Math Class]

Показать описание
This video is not like my normal uploads. This is a supplemental video from one of my courses that I made in case students had to quarantine. This is a follow up to previous videos introducing logic and set theoretic ideas. In this video, we discuss how to extend the set-theoretic counting principles (formulas for the cardinality of a union and the cardinality of the Cartesian product) to the Sum Principle and Product Principle four counting. We seek to give examples of the principles (counting edges in complete graphs and counting nonattacking rook arrangements) as well as to give intuition behind why the formulas work or hold. We also show how to begin to think about combining the two formulas to provide more complex counting arguments.
Note that this video is part of a series kept in a playlist called [Discrete Math Class]:
If you like this video, consider subscribing to my channel and let me know in the comments if you'd like to see more like this.
This textbook for the course is the open-source textbook by Oscar Levin:
0:00 : Elementary Counting Principles
00:11 : Introduction and n non-attacking rooks on nxn chessboard.
01:04 : The Sum Principle
03:25 : The Product Principle
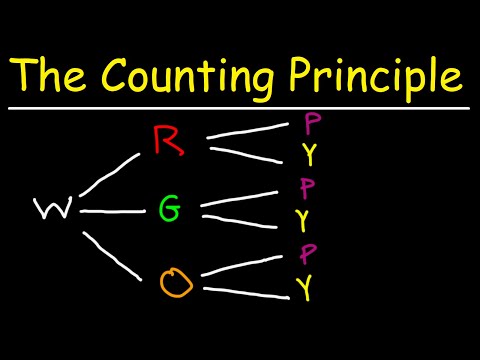
05:45 : Product Principle via Tree diagrams
06:50 : Combining the Principles
08:40 : Revisit non-attacking rooks
10:30 : Non-attacking rooks on rectangular chessboard
#settheory #combinatorics #counting #countingprinciples #sumprinciple #productprinciple #additionprinciple #multiplicationprinciple #combinatorialobjects #union #cartesianproduct #cartesian #math #manim #discretemathematics #rooks #chessboard #venndiagrams #nonattackingrooks #treediagram
To learn more about animating with manim, check out:
_______________________________________
Background Music:
Note that this video is part of a series kept in a playlist called [Discrete Math Class]:
If you like this video, consider subscribing to my channel and let me know in the comments if you'd like to see more like this.
This textbook for the course is the open-source textbook by Oscar Levin:
0:00 : Elementary Counting Principles
00:11 : Introduction and n non-attacking rooks on nxn chessboard.
01:04 : The Sum Principle
03:25 : The Product Principle
05:45 : Product Principle via Tree diagrams
06:50 : Combining the Principles
08:40 : Revisit non-attacking rooks
10:30 : Non-attacking rooks on rectangular chessboard
#settheory #combinatorics #counting #countingprinciples #sumprinciple #productprinciple #additionprinciple #multiplicationprinciple #combinatorialobjects #union #cartesianproduct #cartesian #math #manim #discretemathematics #rooks #chessboard #venndiagrams #nonattackingrooks #treediagram
To learn more about animating with manim, check out:
_______________________________________
Background Music:
Комментарии
 0:09:06
0:09:06
 0:11:26
0:11:26
 0:11:57
0:11:57
 0:07:39
0:07:39
 0:10:52
0:10:52
![[Discrete Mathematics] Counting](https://i.ytimg.com/vi/dnln94G7uC8/hqdefault.jpg) 0:12:56
0:12:56
 0:12:41
0:12:41
 0:10:37
0:10:37
 0:15:49
0:15:49
 0:21:15
0:21:15
 0:17:41
0:17:41
 0:09:23
0:09:23
 0:29:39
0:29:39
 0:11:11
0:11:11
 0:00:33
0:00:33
 0:01:01
0:01:01
 0:05:15
0:05:15
 0:08:23
0:08:23
 0:36:19
0:36:19
 0:11:23
0:11:23
![[Discrete Mathematics] Rule](https://i.ytimg.com/vi/t0us-MXrFZg/hqdefault.jpg) 0:06:00
0:06:00
 1:06:24
1:06:24
 0:16:47
0:16:47
 0:13:26
0:13:26