Modular forms: Hecke operators

preview_player
Показать описание
This lecture is part of an online graduate course on modular forms.

We introduce Hecke operators for modular functions in three different ways.

  1. Richard E Borcherds
  2. Introduction
  3. Complex analysis
Рекомендации по теме
Modular forms: Hecke 0:16:50

Modular forms: Hecke operators

Modular forms: Hecke 0:20:11

Modular forms: Hecke operators for forms

Modular Forms & 1:20:47

Modular Forms & Hecke Operators ☆ Mathematics Lecture

Modular curves, modular 0:50:22

Modular curves, modular forms and Hecke operators: old and new - Winnie Li

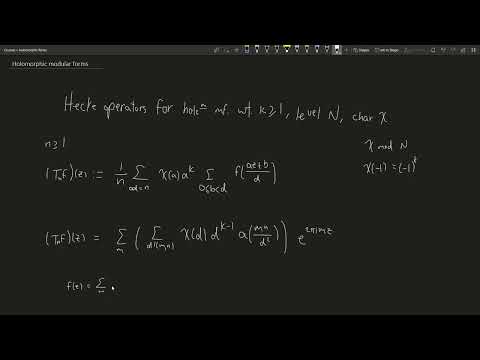
Holomorphic modular forms 0:07:22

Holomorphic modular forms IV: Hecke operators

Workshop On Modular 0:47:19

Workshop On Modular Forms Discussion 1 Hecke operators, Shimura Map

Fermat's Last Theorem: 0:12:30

Fermat's Last Theorem: The Hecke Operators! (3.18, #41)

Fermat's Last Theorem: 0:06:34

Fermat's Last Theorem: Hecke Eigenforms! (3.20, #43)

CDM 2023: Vesselin 0:58:04

CDM 2023: Vesselin Dimitrov: Modular forms and arithmetic algebraization methods I

Fermat's Last Theorem: 0:06:40

Fermat's Last Theorem: Properties of Hecke Operators! (3.19, #42)

John Voight: Computing 0:57:42

John Voight: Computing classical modular forms as orthogonal modular forms

Kalani Thalagoda - 0:32:51

Kalani Thalagoda - Bianchi modular forms

Introduction to Modular 0:21:01

Introduction to Modular Forms - Part 6 of 8

Distributional Aspects of 0:10:46

Distributional Aspects of Hecke Eigenforms - Raphael Steiner

The Congruent Number 0:56:28

The Congruent Number Problem Part VII: The Big Theta Equation, Hecke Operators, and Old/Newforms!

Factorization and Modular 0:49:29

Factorization and Modular Forms

Hecke Traces via 1:13:44

Hecke Traces via Hypergeometric Character Sums - Ling Long, Louisiana State University USA

Jack Davies - 1:02:40

Jack Davies - Derived Hecke operators

Kieran Child - 0:46:04

Kieran Child - Computation of weight 1 modular forms

Derived Hecke Action 1:10:12

Derived Hecke Action For Weight One Modular Forms Via Classicality - Gyujin Oh

Hecke operators 0:13:52

Hecke operators

problem 4-1-4 0:04:26

problem 4-1-4

Abhishek Banerjee: Quasimodular 0:46:05

Abhishek Banerjee: Quasimodular Hecke algebras and Hopf actions

Hilbert modular forms 1:18:57

Hilbert modular forms -II: L-functions - A. Raghuram

Комментарии
Автор

Great lecture. I hope you are well and keep up the good work!

epsilonmath
Автор

Just figured out that Hecke operators do more than what is shown in this video!
So, the video showed that
j(z/2)+j((z+1)/2)+j(2z) is a modular function, but you can also do other constructions with them.

Just take the product of the three fake modular forms!
Since every symmetric expression with them becomes a modular function, you can easily calculate the polynomial with these roots!

This means that you can evaluate j(z/2), simply by solving a third degree polynomial with coefficients polynomials j(z). Cool, right?

The fact that you have to solve a polynomial in j(z) actually implies cool Galois theory... because you basically get a Galois extension of SL(2, p) of the domain (ring) of modular functions, which is equivalent to the domain of polynomials, and proofs that for every prime p, the domain of polynomails has an extension isomorfic with SL(2, p)

Glad I figured this out. Definitely going to try to do more algebra with this!

caspermadlener