Dynamic Mode Decomposition (Overview)

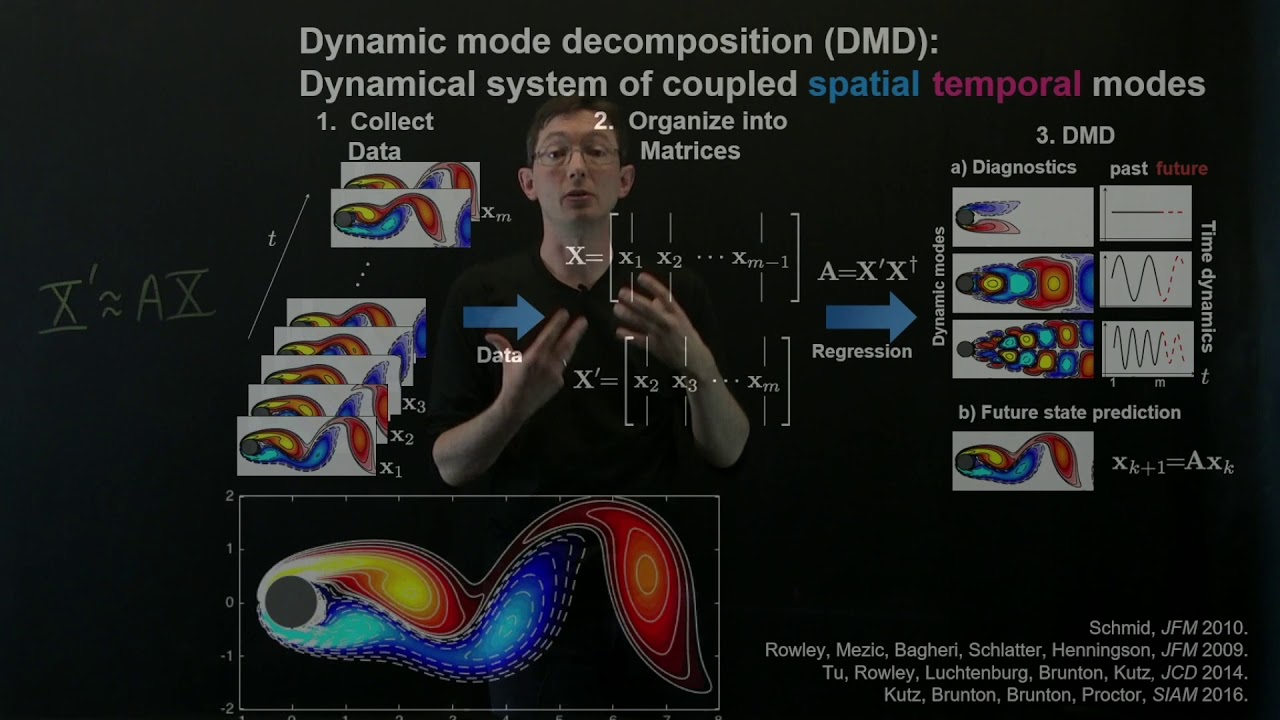
In this video, we introduce the dynamic mode decomposition (DMD), a recent technique to extract spatio-temporal coherent structures directly from high-dimensional data. DMD has been widely applied to systems in fluid dynamics, disease modeling, finance, neuroscience, plasma physics, robotics, and video modeling.

This video was produced at the University of Washington

[noahbarrow]

Junior ME student, who wanted nothing more for their term to be over so I could sit down with these videos, your books and some code. Merry christmas to me!

[juliocardenas]

I just received your book in the mail 📕!
It’s wonderful to watch your lectures along reading your book.
Thank 🙏🏾🧑🏽‍💻

[TungNguyen-gxfy]

NOTE: DMD is a purely data-driven method.
- 1: collect data and create matrix X=[x1 x2 ... x_{m-1}] and X'[x2 x3 ... x_ m] (tall skinny matrices).
- 2: The purpose of DMD is finding A: X' ~ AX. Theoretically, A = X'X^{dagger}, but it's too big, so DMD tries to find A without computing it directly by finding its dominant eigenpairs.
- 3: X = USV*
- 4: X' = AUSV* => X'VS* = AU => U*X'VS* = U*AU = A^ (A^ is the best linear system tell us how POD mode - cols(U) - involves in times)
eigvals(A^) = eigvals(A)
- 5: A^W = WV (W are eigenvectors of A^, V are eigenvalues of A^).
- 6: P = X'VS*W are the eigenvectors of A corresponding to eigenvecors W of A^.
==> Then we have V and P (eigvals(A) and eigvec(A)). Done

[diegoandrade]

for transient problems what is the "fancier" regression Steve is referring to?

[nikoshazaridis]

Hi great video! Can anyone explain, how does one get from the modes and dynamics back to the reconstructions? Any source would be greatly appreciated as I can't seem to find explicit descriptions on the Prof Brunton's books.

[khanhduyphan]

wow, it stunned me. by the way, I am studying EEMD and some other decomposition such as SSA, VMD, and they make me feel extremely puzzled. Hence, would you mind making a video about them, how to use and separate. Thank you so much

[sefabektas]

Hi Sir, really appreciate what you have done, it is a pleasure to learn new methods to combine them with different fields. But, it sometimes might be hard to interpret something when you have just started learning. In the DMD method, I get stuck with the interpretation of modes like decaying oscillating, or growing modes in terms of accuracy of prediction. For example, you don t have an exact equation to check out the modes of the model, instead, just have pure data. And you find a few modes dominating your system considering singular values but some of them growing and others decaying or oscillating. How do you check these modes are convenient for your model? Do decaying and growing modes mean something in your prediction? If they are, until when? How do you decide to cut off the time step for the prediction? Looking forward to hearing from you.

[tomoki-vo]

simular to word masking in NLP. great video

[jyanguas]

Nice video! I just have a question.
Why are the DMD modes considered "spatial"? Where do that spatial features come from? I do not understand how is the spatial information related to the DMD modes.
Is it because the matrices from which we start (X, X') do contain the spatial information? As their columns may be, for example, some EEG time series from different locations

[uchennaogunka]

Can DMD and/or POD be used with only one snapshot (i.e a velocity vector column matrix at one timestep only) to produce the modes and coherent structures at that timestep/snapshot?

[thefieldcto]

Steve, How are you super imposing the images on to the lightboard. I have a lightboard that I use for videos but your images look awesome vs hand drawings, Looks great!

[michaeljanicki]

Should the term at 14:50 lambda^t be lambda^(k*delta_t)?

[juanmanuelpedrosa]

I don't know if you will read this but this is the kind of work that I was talking about, very similar but really nothing like it

[sercanozturk]

Hi Sir, the DMD can be applied on a gust flow problem? You said that "If have strong transients or non-stationary behavior in flow fields, its get more complicated.", Is it current for ın my research case or can it be tried?

[maxfinnian]

It is worth noting that in the case where X and X' are hankel matrices, this is mathematically identical to the Matrix Pencil Method of 1995.

[federicogasparv]

As always, fantastic video. Might I ask if it is possible to adapt the same ideas but for a set of transformations, each of them linear, and each transformation is the best linear aproximation from t_i to t_{i+1}, but the set of transformations itself depends on t and are not linear.

[aaaaaaaaaabbbbbbbbbb]

Can I think of DMD as first order vector autoregression combined with a trick to computationally handle a giant coefficient matrix?

[dr_blerk]

Is a 1-dimensional DMD equivalent to a discrete temporal Fourier Transform?

[johnfinn]

At 18:17 you speak of projecting the n \times n matrix A by the U*AU operation, resulting in a m \times m matrix. But U is unitary (in the sense of U*U=I_m -- but not of course UU*=I_n -- and not just a projection operator. So it projects n-dimension to m-dimension but rotates too, right?

[IlCanaleDiNico]

Hi.
I don't get why projecting A over U should reduce it and return A_tilda. U should be of dimension n x n (so like one million x one million in your example), but you speak as U should have m columns instead....
What am I missing, sir?
Thanks a lot for your work!