Integrating Powers of tanx | Trigonometry

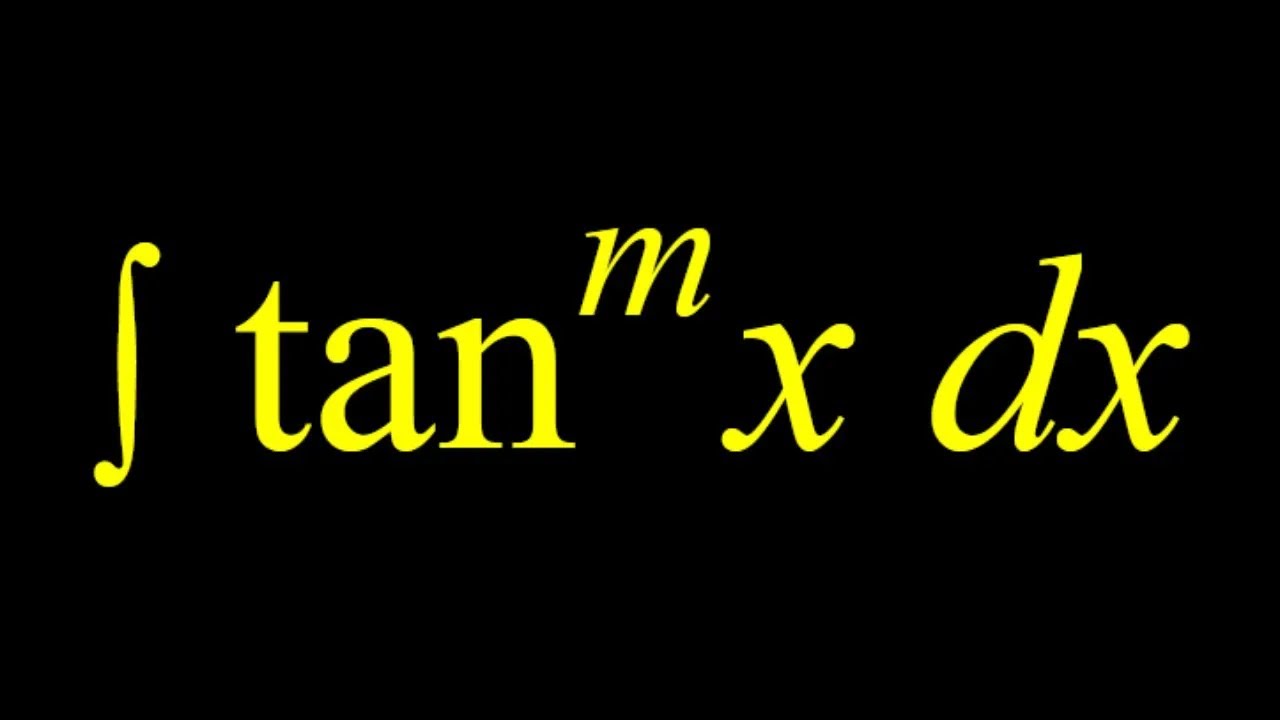
Показать описание

🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡

If you need to post a picture of your solution or idea:
x^3+2x^2=3
#ChallengingMathProblems #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva

PLAYLISTS 🎵 :

SyberMath Shorts

Рекомендации по теме

Комментарии

Honestly i would love to see some more videos abaut integrals on your main chanell or here because integrals are very intetesting topic

janekfortepianek

Good video. I just thought you would be working toward a general solution.

JefiKnight

I think it would be nice to generalize it like in the thumbnail. I generalized it for even and odd powers separately. I have been able to solve it for the odd powers directly, using the binominal theorem, and for the even powers, I found a recursive formula. I analyzed and estimated a explicit formula. I then prooved it via induction.

Dany-wi

2:30 Here I would use the fact that the first derivative of tan(x) = sin(x)/cos(x) can be written in two ways.
According to the quotient rule, the first derivative of tangens is
tan'(x)
= (cos(x)*cos(x) - sin(x)*(- sin(x)) / cos^2(x)
= (cos^2(x) + sin^2(x)) / cos^2(x)
= 1 / cos^2(x) (due to the addition theorem in the numerator) or
= 1 + tan^2(x), which is more useful in this case, since it directly connects the tangens to its derivative.
If we subtract 1, we get
tan^2(x) = tan'(x) - 1
and by integrating both sides:
integral tan^2(x) dx = tan(x) - x + const.
the same result as shown at 3:36.

goldfing

1:00 This kind of integral doesn't need a complicated substitution, because you see that the first derivative of cos(x) is -sin(x) and sin(x) is contained in the integrand, so you can just apply the chain rule for derivatives:
f(g(x))' = f'(g(x)) * g'(x)
and can set f(x) = ln(|x|), g(x) = cos(x), f'(x) = 1/x, g'(x) = -sin(x) and then write
f(g(x)) = ln(|cos(x)|)
f'(g(x))' * g'(x) = 1/cos(x) * (- sin(x)) = -sin(x)/cos(x) = -tan(x)
Therefore
integral tan(x) dx
= - integral -tan(x) dx
= -ln(|cos(x)|).

goldfing

very cool video

I have one question, what software do you use?

leonardobarrera

Great video on integration ! Just a question: which of your accounts prevail ?

paultoutounji

I enjoy your video please continue power of tanx

mahdiali

Dear friend, do you use tablet for write? Do you use some software ? It is excelent.🇧🇷🇧🇷🇧🇷🇧🇷

paulor.r.correia

Integrating Powers of tanx | Trigonometry

Integrating powers of tan x

Integrating powers of tan(x)

Integrating Powers of tanx | Trigonometry

Integrating Powers of tan(x) and sec(x) with an Even Power of sec(x)

STANDARD Integration of powers of tanx

trig integrals involving secant and tangent (calculus 2)

Trigonometric Integrals: Powers of Secant and Tangent

Integrating Powers of Tangent

Integral of tan^5(x)

Ma 126 Integrating powers of the tangent function.

Integral of tan^4x

Trig Integrals (Integrating Powers of Tangent)

Trigonometric Integrals Powers of Secant and Tangent tan^4(x)

Powers of tan(x) and sec(x)

Section 3.2 (Integrating Products of Powers of tan x and sec x)

How to Integrate Odd & Even Powers of Sine & Cosine : Math Problems & Trigonometry

Integration : - ( Integral of even powers of Tanx and Cotx ) - 23.

8.3.4 Integrating Products of Powers of Secant and Tangent

Integrating Powers of Trigonometric Functions--Power of the Tangent is Odd and Positive

Trig Integrals Involving Even Powers of Tan and no Factors of Sec

INTEGRALS OF POWERS OF TANGENTS AND SECANTS: CASE 1

Integrating Even Powers of sin(x) and cos(x)

Integrating the Products of the Powers of Secant and Tangent | Odd and Even Powers

integral of tan^2(x)*sec(x), calculus 2 tutorial