filmov
tv
Quadratic Word Problems: Projectile Motion
Показать описание
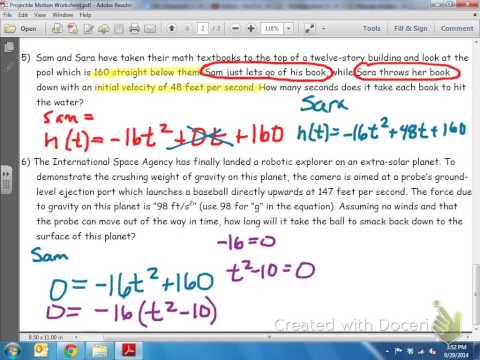
A ball is thrown into the air with an upward velocity of 12 ft/sec. The
equation for the ball’s height (h) at any time (t) is h(t) = -4t^2 + 12t + 5.
(a) Find the maximum height attained by the ball.
(b) Find the time at which the ball reaches the ground.
(c) Find the time(s) at which the ball reaches a height of 10 ft.
___________________________________________________________________________
Disclaimer: To be technically correct in terms of a ball being thrown on Earth, the coefficient for the t^2-term in the equation for h(t) would have to be -16 (due to Earth's gravity). I chose the number -4 instead to keep the numbers/calculations small, since the focus of the video is more so on working with quadratic equations than modeling real-life projectile motion. For the equation I use in this problem, I am assuming that the ball is being thrown from a height of 5 feet and that the ball is under a gravitational influence of 8 ft/s^2 (Earth's gravity is 32 ft/s^2, but that's not the focus of the problem).
equation for the ball’s height (h) at any time (t) is h(t) = -4t^2 + 12t + 5.
(a) Find the maximum height attained by the ball.
(b) Find the time at which the ball reaches the ground.
(c) Find the time(s) at which the ball reaches a height of 10 ft.
___________________________________________________________________________
Disclaimer: To be technically correct in terms of a ball being thrown on Earth, the coefficient for the t^2-term in the equation for h(t) would have to be -16 (due to Earth's gravity). I chose the number -4 instead to keep the numbers/calculations small, since the focus of the video is more so on working with quadratic equations than modeling real-life projectile motion. For the equation I use in this problem, I am assuming that the ball is being thrown from a height of 5 feet and that the ball is under a gravitational influence of 8 ft/s^2 (Earth's gravity is 32 ft/s^2, but that's not the focus of the problem).
0:57:09
Quadratic Word Problems (practice problems)
0:11:35
Quadratic Word Problems: Projectile Motion
0:03:24
A Projectile Problem Using Quadratics - Example 1
0:11:55
Solving Projectile Motion Word Problems Using Quadratics
0:03:55
Quadratic word problem — projectile motion #1
0:13:12
Algebra 1: Projectile Motion
0:15:01
Quadratic Applications: Projectile Motion Problems (part 1)
0:14:01
Quadratic Word Problems - Projectile Motion
0:05:58
Maximum and Minimum Value Word Problems - Quadratic Equations
0:12:14
Quadratic Word Problems - Projectile Motion
0:03:35
Quadratic word problem — projectile motion #2
0:05:53
Example 4: Applying the quadratic formula | Quadratic equations | Algebra I | Khan Academy
0:19:20
Algebra 1AB: Solving Projectile Motion Word Problems (Quadratics)
0:03:16
Projectile Word Problem - Height of an Object - Application Involving a Quadratic Equation
0:19:55
Quadratics Word Problems: area and projectile motion
0:11:23
Quadratic Projectile Motion Problem
0:05:55
Common Core Math: Projectile Motion Quadratic Equation
0:20:45
Projectile Motion Word Problems
0:06:48
Solving a Projectile Problem Using Quadratics - Example 2
0:25:54
0.10 Precalculus Quadratic Word Problems (Projectile Motion)
0:02:30
Quadratic equations word problem: Projectile
0:04:48
Projectile motion word problem for quadratics
0:04:05
How to Solve Projectile Motion Word Problems - Quadratic Functions
0:07:40
Quadratic function example with projectile motion
Комментарии