filmov
tv
Suppose A_1,A_2,….,A_30 are thirty sets eachhaving 5 elements with no common element across the
Показать описание
Suppose A_1,A_2,….,A_30 are thirty sets each
having 5 elements with no common element across the sets and B_1,B_2,…..,B_n are n sets each having 3 elements with no common element across the sets. Let ⋃_(i=1)^30▒〖A_i=⋃_(j=1)^n▒〖B_j=S〗〗 and each element of S belong to exactly 10 of A_j's and exactly 9 of B_j's. The value of n is equal to
(a) 15
(b) 30
(c) 40
(d) 45
Downloads our APP for FREE Study Material ,Video Class ,Test paper & Mock test etc...
Click to Download Impetus Gurukul Free Learning App here
To buy complete Course please Visit–
join Impetus Gurukul live classes via the official Website:
Our Social links
having 5 elements with no common element across the sets and B_1,B_2,…..,B_n are n sets each having 3 elements with no common element across the sets. Let ⋃_(i=1)^30▒〖A_i=⋃_(j=1)^n▒〖B_j=S〗〗 and each element of S belong to exactly 10 of A_j's and exactly 9 of B_j's. The value of n is equal to
(a) 15
(b) 30
(c) 40
(d) 45
Downloads our APP for FREE Study Material ,Video Class ,Test paper & Mock test etc...
Click to Download Impetus Gurukul Free Learning App here
To buy complete Course please Visit–
join Impetus Gurukul live classes via the official Website:
Our Social links
0:06:55
A1,A2,.....,A30 are thirty sets each with 5 elements and B1,B2,.....Bn, are n sets each with 3...
0:11:19
Suppose A1, A2,...., A30 are thirty sets each having 5 elements and B1, B2,...., Bn are n sets
0:02:46
Suppose `a_1,A_2,.....,A_30` are thirty sets each with five elements and `B_1, B_2,.......,B_n...
0:04:21
Suppose \( A_{1}, A_{2}, \ldots, A_{30} \) are thirty sets each having 5 elements and \( B_{1}, ...
0:03:42
26 suppose A1,A2,A3...A30 are thirty sets each having 5 elements and B1,B2,...Bn are n sets class 11
0:03:40
Suppose \( A_{1}, A_{2}, A_{3}, \ldots \ldots, A_{30} \) are thirty...
0:09:36
Suppose A1A2 A30 are thirty sets Question 29 NCERT Exemplar Class 11 Chapter 1 Sets
0:08:55
Suppose A1,A2,...A3 are thirty sets each with five elements and ||class 11 rd sharma chapter 1 sets
0:03:26
Suppose A_1,A_2,….,A_30 are thirty sets eachhaving 5 elements with no common element across the
0:01:45
Suppose A1,A2,....,A30 are thirty sets, each having 5 elements and B1,B2,.....,Bn are n sets..#Sets...
0:03:55
Suppose A1,A2,..A30 are 30 set each with 5 elements and B1,B2,..Bn are 'n'. Set each with ...
0:05:19
suppose p1,p2..p30 are 30 sets each having 5 elements and q1,q2..qn are n sets with 3 element each.
0:10:45
Set Theory : Let each Xi contains 10 elements and each Yi contains 6 elements....
0:20:19
Class 11| Chapter 1| Set | Important Question bases on Union|
0:25:32
Sets (Q29 ncert exemplar Suppose A1,A2,...,An are) cbse class 11
0:08:06
Important question on Set for JEE main+advanced| By Er. Deepak pandey Sir
0:17:41
Permutations and Combinations Tutorial
0:08:16
Each set \( X \), contains 5 elements and each set \( Y \), contains 2 elements and \( \bigcup_{...
2:03:18
Peppa Pig Tales 🐷 April Fool's Day! 🐷 Peppa Pig Videos
0:11:37
SETS CLASS 11 PART 36
0:00:45
The Psychology of Sun Tzu In The Art Of War
0:06:06
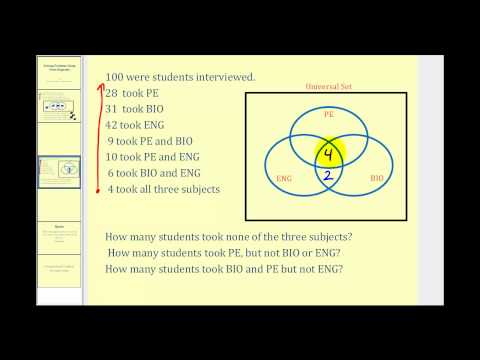
Solving Problems with Venn Diagrams
0:03:31
JEE Main 2020 9 Jan Shift 2 Maths Q9 Solution Sets and Relation
1:04:07
Peppa Pig Full Episodes | New Peppa Pig | Peppa Pig 2020 | Kids Videos
Комментарии