filmov
tv
Physics 68 Lagrangian Mechanics (4 of 25) Free Fall: Example

Показать описание
In this video I will derive the position with-respect-to time equation of a simple free-fall problem using the partial derivative of Lagrangian equation.
Next video in this series can be seen at:
Physics 68 Lagrangian Mechanics (4 of 25) Free Fall: Example
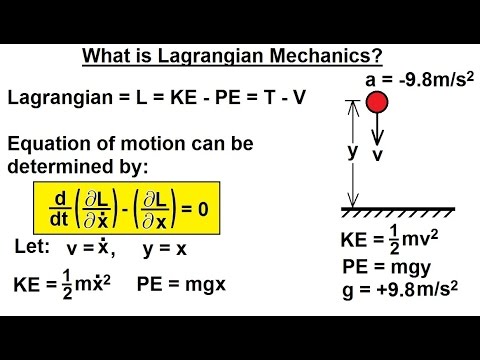
Physics 68 Lagrangian Mechanics (1 of 25) What is Lagrangian Mechanics?
Physics 68 Lagrangian Mechanics (3 of 25) The Partial Derivative W.R.T. Position
Physics 68 Lagrangian Mechanics (2 of 25) Why Does the Lagrangian Equation Work?
Physics 68 Lagrangian Mechanics (11 of 25) The Compound Atwood Machine (1 of 3)
Physics 68 Lagrangian Mechanics (6 of 25) Simple Harmonic Motion: Method 1
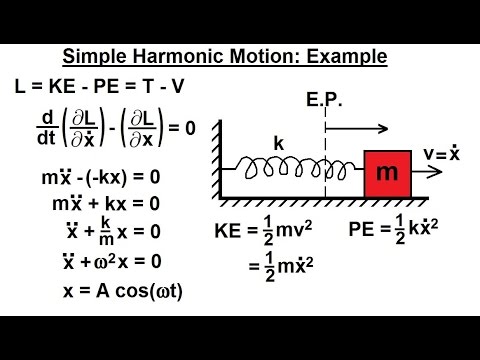
Physics 68 Lagrangian Mechanics (5 of 25) Simple Harmonic Motion: Example
Physics 68 Lagrangian Mechanics (9 of 25) Example: The Atwood Machine (with Mass)
Physics 68 Lagrangian Mechanics (8 of 25) Example: The Atwood Machine
Physics 68 Lagrangian Mechanics (14 of 25) Pendulum w/ Oscillating Fulcrum (Part 1 of 2)
Lagrangian Mechanics Part 4: Atwood Machine
Physics 68 Lagrangian Mechanics (7 of 25) Simple Harmonic Motion: Method 2
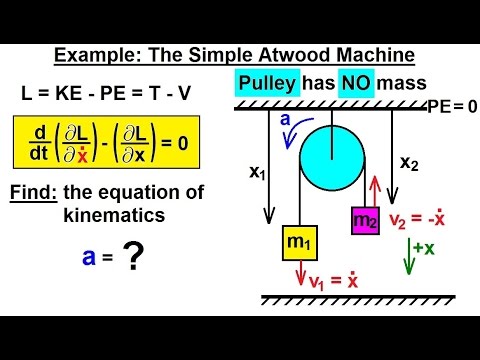
Physics 68 Lagrangian Mechanics (10 of 25) The Atwood Machine
Physics 68 Lagrangian Mechanics (19 of 32) Oscillating Bar
Newtonian VS Lagrangian Mechanics #Shorts
Physics 68 Lagrangian Mechanics (16 of 25) Rolling Disk Attached to Spring
Chap 4.5. Lagrangian mechanics - example 1 - mass over a pulley
Lagrangian v Newtonian Formalisms
Physics 68 Lagrangian Mechanics (17 of 32) Example: Rolling Disk
Solving Atwood's Machine With Lagrangian Mechanics
Physics 68 Lagrangian Mechanics (21 of 32) Pendulum with Rotating Disk
LAGRANGIAN Mechanics of PENDULUM
Physics 68 Lagrangian Mechanics (12 of 25) The Compound Atwood Machine (2 of 3)
Lagrangian Dynamics 4
Комментарии
 0:08:51
0:08:51
 0:09:06
0:09:06
 0:05:09
0:05:09
 0:06:08
0:06:08
 0:13:23
0:13:23
 0:09:05
0:09:05
 0:03:13
0:03:13
 0:09:25
0:09:25
 0:06:54
0:06:54
 0:08:25
0:08:25
 0:05:52
0:05:52
 0:10:30
0:10:30
 0:07:10
0:07:10
 0:13:13
0:13:13
 0:01:00
0:01:00
 0:06:25
0:06:25
 0:07:42
0:07:42
 0:45:10
0:45:10
 0:05:49
0:05:49
 0:12:42
0:12:42
 0:04:56
0:04:56
 0:32:03
0:32:03
 0:09:33
0:09:33
 0:19:13
0:19:13