filmov
tv
Daniel Ratliff - Modulation of Multiperiodic Wavetrains leading to Nonlinear Wave Equations

Показать описание
Title: Modulation of Multiperiodic Wavetrains leading to Nonlinear Wave Equations
Abstract:
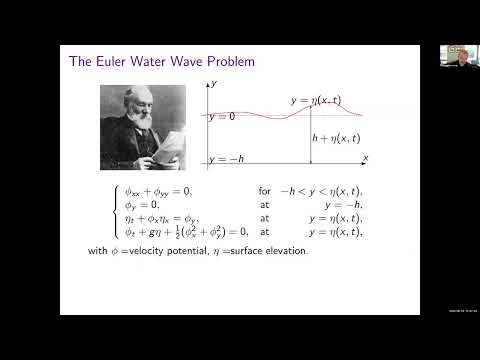
The study of the Whitham equations for multiperiodic wavetrains (or in general, multiparameter relative equilibria) has been studied in the past (for example, Ablowitz, Benney and Ablowitz), however there has been little discussion up to now as to how they morph at the elliptic-hyperbolic transition point. The aim of this talk is to show not only how nonlinear PDEs emerge at this transition, but that the form of their coefficients are tied to the geometry of the conservation laws.
We begin with an overview of the constructs involved, such as the relevant multisymplectic framework, the modulation approach and the derivation of the linearised Whitham system. Following this, the degeneracy of the Whitham system is formulated using the breakdown of the conservation laws and related to the emergence of both the KdV and two-way Boussinesq via the modulation approach. In particular, these systems have coefficients that can be determined a priori from either the conservation laws themselves or from an elementary linear operator analysis. These ideas are then demonstrated for two examples of physical interest – two layered shallow water hydrodynamics and a coupled NLS model (which can be used to study rogue waves and Bose-Einstein condensates).
The work presented is joint work with Prof. Tom Bridges (University of Surrey).
Abstract:
The study of the Whitham equations for multiperiodic wavetrains (or in general, multiparameter relative equilibria) has been studied in the past (for example, Ablowitz, Benney and Ablowitz), however there has been little discussion up to now as to how they morph at the elliptic-hyperbolic transition point. The aim of this talk is to show not only how nonlinear PDEs emerge at this transition, but that the form of their coefficients are tied to the geometry of the conservation laws.
We begin with an overview of the constructs involved, such as the relevant multisymplectic framework, the modulation approach and the derivation of the linearised Whitham system. Following this, the degeneracy of the Whitham system is formulated using the breakdown of the conservation laws and related to the emergence of both the KdV and two-way Boussinesq via the modulation approach. In particular, these systems have coefficients that can be determined a priori from either the conservation laws themselves or from an elementary linear operator analysis. These ideas are then demonstrated for two examples of physical interest – two layered shallow water hydrodynamics and a coupled NLS model (which can be used to study rogue waves and Bose-Einstein condensates).
The work presented is joint work with Prof. Tom Bridges (University of Surrey).
 0:50:32
0:50:32
 0:28:58
0:28:58
 0:46:13
0:46:13
 0:35:55
0:35:55
 0:29:46
0:29:46
 0:57:11
0:57:11
 0:09:31
0:09:31
 0:12:23
0:12:23
 1:20:59
1:20:59
 0:09:41
0:09:41
 0:21:52
0:21:52
 0:14:03
0:14:03
 0:19:58
0:19:58
 0:57:49
0:57:49
 0:07:38
0:07:38
 0:21:43
0:21:43
 0:37:12
0:37:12
 1:04:51
1:04:51
 0:19:06
0:19:06
 0:10:33
0:10:33
 0:01:11
0:01:11
 0:07:58
0:07:58
 1:04:47
1:04:47
 0:12:03
0:12:03