filmov
tv
Germany | A nice Algebra Problem | Math Olympiad

Показать описание
#algebra #exponent#olympiad #simplification#exam
Hello, my beloved family! 😍😍😍
I hope everyone is doing great! 😲 😲😲
If you enjoyed this video on How to solve this Math Olympiad problem, please show your support by liking and subscribing to my channel. Your support means the world to me! 😊😊😊
#matholympiad
#algebra
#mathematics
#maths
#math
#olympiad
#matholympiad #algebra#math#simplification #Exponents#vedicmath#viralmathproblem #howto#mathematics #mathematicslesson#calculus
improve math speed
France math Olympiad
Germany math Olympiad
Japanese math Olympiad
china math Olympiad
math Olympiad questions
maths Olympiad
France math Olympiad
math Olympiad
maths Olympiad questions
Japanese multiplication method
math
math Olympiad problems
math problem
algebra 2
nice olympiad Math Problem
Olympiad mathematics
Olympiad questions
Olympic math
Math Olympiad | A Nice Algebra Problem | How to solve this problem
A Nice Math Olympiad Algebra Problem
A Nice Exponents Problem
A Nice Math Olympiad Exponential Problem
Olympiad Algebra
Solving quartic equation
Solving A Quadratic Equations
International Math Olympiad Problem
International Math Olympiad Problem,
math olympiad topics
olympiad preparation
international olympiad maths
olympiad mathematics
international olympiads
international maths olympiad
olympiad
junior math olympiad
international mathematics olympiad
mathematics
math olympiad
international math olympiad 2024
international math olympiad
math olympiad problem
math olympiad preparation
american math olympiad question
math olympiad questions
math olympiad question
math olympiad problem
olympiad mathematics
math olympiad
math olympiad training
Canada maths olympiad
Malaysia math olympiad problems
math olympiad preparation
math olympiad questions
math olympiad algebra problem
maths olympiad
olympiad, mathematical olympiad
france math olympiad question
olympiad math problems
france maths olympiad preparation
olympiad math
maths trick
math olympiad algebra
france math olympiad questions
high school math
France | Can You Solve this ? Math Olympiad
can you solve this complex problem?
can you solve this logic puzzle?
can you solve this olympiad question?
olympiad
maths olympiad
olympiad mathematics
math olympiad
math olympiad question
math olympiad questions
mathematical olympiad
math olympiad training
math olympiad preparation
math olympiad problem
olympiad math
math olympiad algebra problem
math olympiad problems
olympiad math problems
maths
france maths olympiad
Luxembourg- Math Olympiad Questions
thailand junior maths olympiad problem
olympiad math problems
beautiful algebra problem
viral math problem
math olympiad problem
Nice Algebra Math Simplification Find Value of X
Russian Math Olympiad Question.
Japanese | Can you solve this ? | Math Olympiad
Nice Exponent Math Simplification
Math Olympiad | A Nice Algebra Problem | How to solve for X and Y in this Problem?
Japanese Math Olympiad Question | A Nice Algebra Problem
UK | Can you solve this ?| Math Olympiad
Japanese Math Olympiad | Calculators Not allowed !
France Math Olympiad | Calculator Not Allowed!
Germany| Can you solve this ? |A Nice Maths Olympiad problem
China | Can you solve this ? Math Olympiad
France | Can you solve this ? | Math Olympiad
Iran Math Olympiad - Algebra - Find f(0)?
France Math Olympiad | Calculator Not Allowed
Russian- Math Olympiad Question
International Maths Olympiad Problem | Alg.Nice Algebra Math Simplification Find Value of X
Russian Math Olympiad Question.
Japanese | Can you solve this ? | Math Olympiad
Nice Exponent Math Simplification
Math Olympiad | A Nice Algebra Problem | How to solve for X and Y in this Problem?
Japanese Math Olympiad Question | A Nice Algebra Problem
France | Can you solve this ?| Math Olympiad
Japanese Math Olympiad | Calculators Not allowed !
France Math Olympiad | Calculator Not Allowed!
Germany| Can you solve this ? |A Nice Maths Olympiad problem
China | Can you solve this ? Math Olympiad
A Nice Math Olympiad Question
Germany| Can you solve this ? |A Nice Math Olympiad
Math Olympiad | A Nice Algebra Problem | How to solve this problem
A Nice Math Olympiad Algebra Problem
A Nice Exponents Problem
A Nice Math Olympiad Exponential Problem
viral math problem,
math Olympiad problem
Math Olympiad Question | Equation Solving| You should know this trick!!
Japanese -A Nice Math Olympiad Problem
- Math Olympiad Problem | You should know this trick!!
Viral Math Olympiad Problem | How to solve
Algebra - Nice Math Olympiad Problem #maths
US Math Olympiad problem #maths
Nice Exponent Math Simplification | Find the value of X??
Math Olympiad Question | Nice Algebraic Equations
math Olympiad problems ! viral math problems
Brazil Maths Olympiad Question #maths #superacademy247
Math Olympiad Question | Algebra
A Nice Chinese Olympiad Exponential Problem
Hello, my beloved family! 😍😍😍
I hope everyone is doing great! 😲 😲😲
If you enjoyed this video on How to solve this Math Olympiad problem, please show your support by liking and subscribing to my channel. Your support means the world to me! 😊😊😊
#matholympiad
#algebra
#mathematics
#maths
#math
#olympiad
#matholympiad #algebra#math#simplification #Exponents#vedicmath#viralmathproblem #howto#mathematics #mathematicslesson#calculus
improve math speed
France math Olympiad
Germany math Olympiad
Japanese math Olympiad
china math Olympiad
math Olympiad questions
maths Olympiad
France math Olympiad
math Olympiad
maths Olympiad questions
Japanese multiplication method
math
math Olympiad problems
math problem
algebra 2
nice olympiad Math Problem
Olympiad mathematics
Olympiad questions
Olympic math
Math Olympiad | A Nice Algebra Problem | How to solve this problem
A Nice Math Olympiad Algebra Problem
A Nice Exponents Problem
A Nice Math Olympiad Exponential Problem
Olympiad Algebra
Solving quartic equation
Solving A Quadratic Equations
International Math Olympiad Problem
International Math Olympiad Problem,
math olympiad topics
olympiad preparation
international olympiad maths
olympiad mathematics
international olympiads
international maths olympiad
olympiad
junior math olympiad
international mathematics olympiad
mathematics
math olympiad
international math olympiad 2024
international math olympiad
math olympiad problem
math olympiad preparation
american math olympiad question
math olympiad questions
math olympiad question
math olympiad problem
olympiad mathematics
math olympiad
math olympiad training
Canada maths olympiad
Malaysia math olympiad problems
math olympiad preparation
math olympiad questions
math olympiad algebra problem
maths olympiad
olympiad, mathematical olympiad
france math olympiad question
olympiad math problems
france maths olympiad preparation
olympiad math
maths trick
math olympiad algebra
france math olympiad questions
high school math
France | Can You Solve this ? Math Olympiad
can you solve this complex problem?
can you solve this logic puzzle?
can you solve this olympiad question?
olympiad
maths olympiad
olympiad mathematics
math olympiad
math olympiad question
math olympiad questions
mathematical olympiad
math olympiad training
math olympiad preparation
math olympiad problem
olympiad math
math olympiad algebra problem
math olympiad problems
olympiad math problems
maths
france maths olympiad
Luxembourg- Math Olympiad Questions
thailand junior maths olympiad problem
olympiad math problems
beautiful algebra problem
viral math problem
math olympiad problem
Nice Algebra Math Simplification Find Value of X
Russian Math Olympiad Question.
Japanese | Can you solve this ? | Math Olympiad
Nice Exponent Math Simplification
Math Olympiad | A Nice Algebra Problem | How to solve for X and Y in this Problem?
Japanese Math Olympiad Question | A Nice Algebra Problem
UK | Can you solve this ?| Math Olympiad
Japanese Math Olympiad | Calculators Not allowed !
France Math Olympiad | Calculator Not Allowed!
Germany| Can you solve this ? |A Nice Maths Olympiad problem
China | Can you solve this ? Math Olympiad
France | Can you solve this ? | Math Olympiad
Iran Math Olympiad - Algebra - Find f(0)?
France Math Olympiad | Calculator Not Allowed
Russian- Math Olympiad Question
International Maths Olympiad Problem | Alg.Nice Algebra Math Simplification Find Value of X
Russian Math Olympiad Question.
Japanese | Can you solve this ? | Math Olympiad
Nice Exponent Math Simplification
Math Olympiad | A Nice Algebra Problem | How to solve for X and Y in this Problem?
Japanese Math Olympiad Question | A Nice Algebra Problem
France | Can you solve this ?| Math Olympiad
Japanese Math Olympiad | Calculators Not allowed !
France Math Olympiad | Calculator Not Allowed!
Germany| Can you solve this ? |A Nice Maths Olympiad problem
China | Can you solve this ? Math Olympiad
A Nice Math Olympiad Question
Germany| Can you solve this ? |A Nice Math Olympiad
Math Olympiad | A Nice Algebra Problem | How to solve this problem
A Nice Math Olympiad Algebra Problem
A Nice Exponents Problem
A Nice Math Olympiad Exponential Problem
viral math problem,
math Olympiad problem
Math Olympiad Question | Equation Solving| You should know this trick!!
Japanese -A Nice Math Olympiad Problem
- Math Olympiad Problem | You should know this trick!!
Viral Math Olympiad Problem | How to solve
Algebra - Nice Math Olympiad Problem #maths
US Math Olympiad problem #maths
Nice Exponent Math Simplification | Find the value of X??
Math Olympiad Question | Nice Algebraic Equations
math Olympiad problems ! viral math problems
Brazil Maths Olympiad Question #maths #superacademy247
Math Olympiad Question | Algebra
A Nice Chinese Olympiad Exponential Problem
Комментарии
 0:08:05
0:08:05
 0:11:55
0:11:55
 0:06:47
0:06:47
 0:07:32
0:07:32
 0:08:14
0:08:14
 0:09:56
0:09:56
 0:08:14
0:08:14
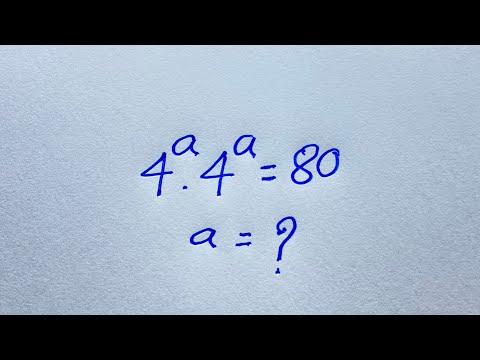 0:05:56
0:05:56
 0:05:02
0:05:02
 0:10:41
0:10:41
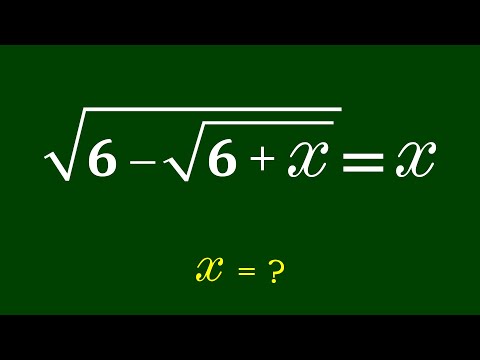 0:22:50
0:22:50
 0:08:49
0:08:49
 0:07:30
0:07:30
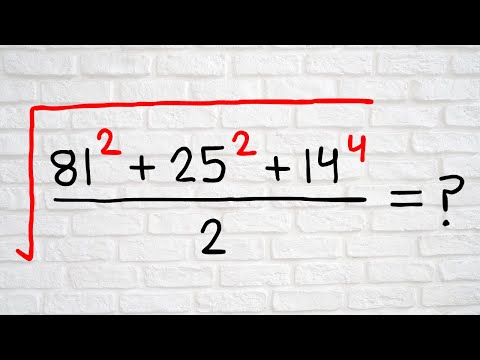 0:10:01
0:10:01
 0:07:19
0:07:19
 0:06:31
0:06:31
 0:07:13
0:07:13
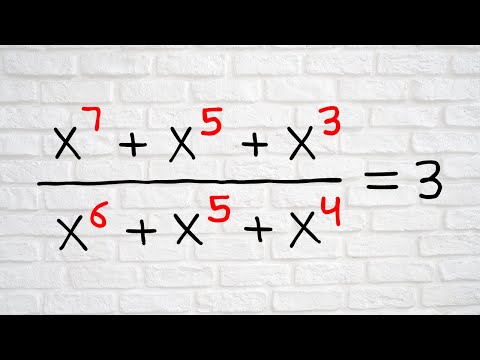 0:12:45
0:12:45
 0:06:28
0:06:28
 0:13:10
0:13:10
 0:06:46
0:06:46
 0:12:39
0:12:39
 0:11:12
0:11:12
 0:09:50
0:09:50