filmov
tv
Matrix methods for systems of differential equations

Показать описание
I show how to use matrix methods to solve first order systems of differential equations. The ideas involve diagonalization and basic linear ODEs.
The example shown involves symmetric matrices.
The example shown involves symmetric matrices.
Simultaneous Equations Matrix Method : ExamSolutions
Gaussian Elimination & Row Echelon Form
Solving System of Linear Equations: Matrix Inversion
Systems of linear first-order odes | Lecture 39 | Differential Equations for Engineers
Matrices - System of Linear Equations (Part 1) | Don't Memorise
Solving Matrix Equations
Matrix Systems of Differential Equations
Gauss Jordan Elimination & Reduced Row Echelon Form
Computational Finance - Video 10 - Gauss-Jacobi method
Matrix inversion method
Solve by Matrix Method | Matrix Method | Matrices | MindYourChoices @mindyourchoices
Matrix methods for systems of differential equations
Manipulating Matrices: Elementary Row Operations and Gauss-Jordan Elimination
Cramer's Rule - 3x3 Linear System
How to use the MATRIX method to solve SIMULTANEOUS equations #3x3
Solve a System of Linear Equations Using LU Decomposition
Solving Linear Systems in three Variables using Matrix Methods Practice Test Full Solutions
Matrix Method to Calculate Circular Convolution
Thomas Algorithm | Solution for tri diagonal system of equations|Tri-Diagonal Matrix 4x4|Mathspedia|
Matrix Class 12 | Solve By Row Equivalent Matrix Method @mindyourchoices
Matrix inverse method || matrix inverse 3x3
🟢06c - Jacobi Iteration Method in Matrix Form: Example 1
Solution of system of linear equation using matrix method interesting example(PART-3)
SOLVING SIMULTANEOUS EQUATION OF 3 UNKNOWN BY INVERSE MATRIX METHOD
Комментарии
 0:09:23
0:09:23
 0:18:40
0:18:40
 0:13:37
0:13:37
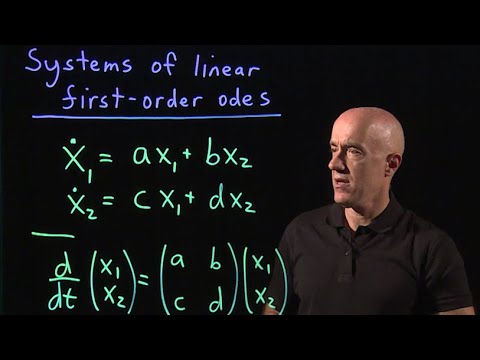 0:08:28
0:08:28
 0:04:04
0:04:04
 0:06:31
0:06:31
 0:24:58
0:24:58
 0:10:51
0:10:51
 0:11:19
0:11:19
 0:12:47
0:12:47
 0:05:23
0:05:23
 0:24:26
0:24:26
 0:10:36
0:10:36
 0:15:03
0:15:03
 0:18:06
0:18:06
 0:08:23
0:08:23
 0:50:19
0:50:19
 0:07:11
0:07:11
 0:21:04
0:21:04
 0:10:40
0:10:40
 0:19:17
0:19:17
 0:21:03
0:21:03
 0:06:41
0:06:41
 0:14:30
0:14:30