filmov
tv
Mastering Forward Difference Tables: A Step-by-Step Guide' || #shorts #viral #mathsclass #mathsadda
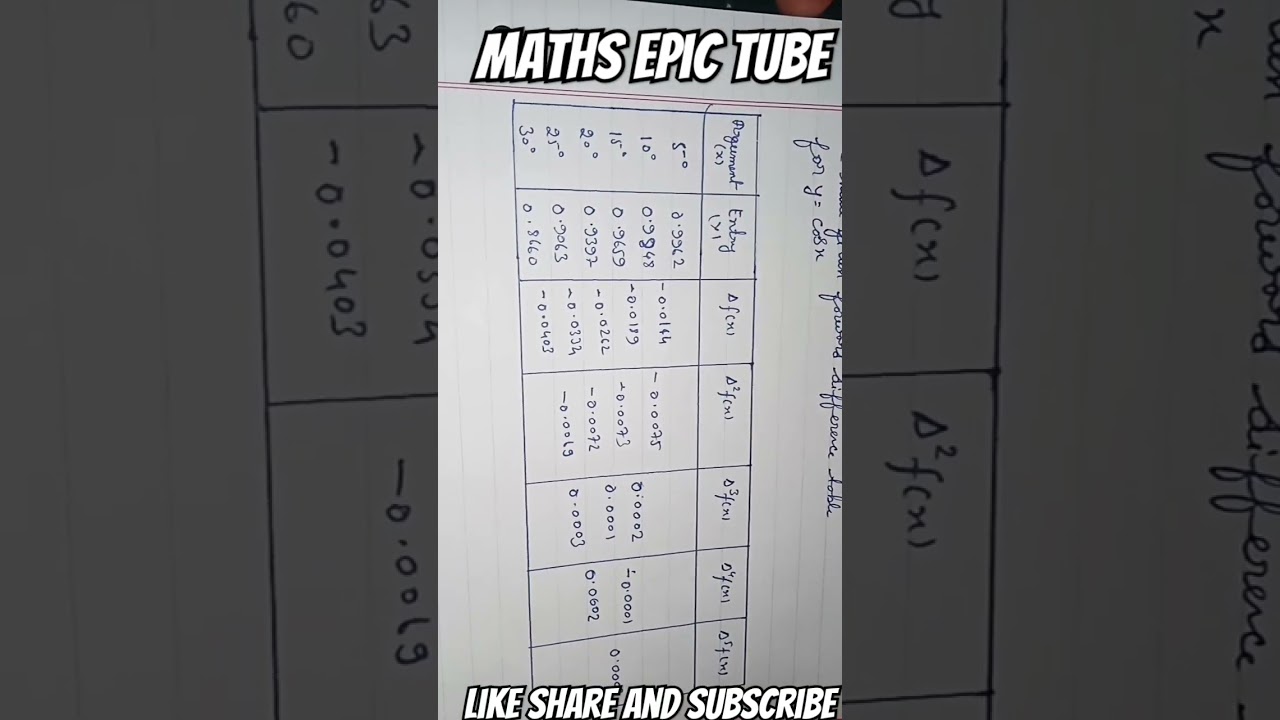
Показать описание
A forward difference table is a method used in calculus and numerical analysis to find the differences between consecutive values of a function. It's often used to approximate derivatives or to generate polynomial approximations for a given set of data points.
To construct a forward difference table, follow these steps:
Start with a set of data points (x, y), where 'x' represents the independent variable and 'y' represents the function values at those points.
Arrange the data points in ascending order based on the 'x' values.
Create a table with columns for 'x' and 'y'. Place the data points in their respective columns.
Add a new column for the first forward difference (Δy) by calculating the difference between consecutive 'y' values. Δy = y[i+1] - y[i].
Continue adding new columns for higher-order differences, such as second forward difference (Δ²y), third forward difference (Δ³y), and so on. Each new column involves calculating the differences between consecutive values in the previous column.
Keep filling in the differences until you observe a pattern or until you reach a column where all values are the same (indicating a constant difference).
The first column (Δy) represents the first-order forward differences, which can be used to approximate the first derivative of the function.
Higher-order differences can be used to generate polynomial approximations for the function.
Remember that constructing a forward difference table might involve a bit of repetitive arithmetic, so using spreadsheet software like Excel or online calculators can simplify the process.
#MathTutorial #DifferentialCalculus #ForwardDifferenceTable #MathematicsEducation #LearnMath #MathHelp #CalculusExplained #MathematicsTutorial
To construct a forward difference table, follow these steps:
Start with a set of data points (x, y), where 'x' represents the independent variable and 'y' represents the function values at those points.
Arrange the data points in ascending order based on the 'x' values.
Create a table with columns for 'x' and 'y'. Place the data points in their respective columns.
Add a new column for the first forward difference (Δy) by calculating the difference between consecutive 'y' values. Δy = y[i+1] - y[i].
Continue adding new columns for higher-order differences, such as second forward difference (Δ²y), third forward difference (Δ³y), and so on. Each new column involves calculating the differences between consecutive values in the previous column.
Keep filling in the differences until you observe a pattern or until you reach a column where all values are the same (indicating a constant difference).
The first column (Δy) represents the first-order forward differences, which can be used to approximate the first derivative of the function.
Higher-order differences can be used to generate polynomial approximations for the function.
Remember that constructing a forward difference table might involve a bit of repetitive arithmetic, so using spreadsheet software like Excel or online calculators can simplify the process.
#MathTutorial #DifferentialCalculus #ForwardDifferenceTable #MathematicsEducation #LearnMath #MathHelp #CalculusExplained #MathematicsTutorial
 0:00:15
0:00:15
 0:23:06
0:23:06
 0:08:10
0:08:10
 0:06:38
0:06:38
 0:14:03
0:14:03
 0:05:21
0:05:21
 0:06:31
0:06:31
 0:06:49
0:06:49
 0:00:16
0:00:16
 0:14:15
0:14:15
 0:25:09
0:25:09
 0:00:43
0:00:43
 0:00:58
0:00:58
 0:00:25
0:00:25
 0:00:32
0:00:32
 0:24:39
0:24:39
 0:51:07
0:51:07
 1:20:42
1:20:42
 0:12:48
0:12:48
 0:00:32
0:00:32
 0:00:28
0:00:28
 0:01:00
0:01:00
 0:04:42
0:04:42
 0:00:31
0:00:31