filmov
tv
A Fusion Formula for Cohomology

Показать описание
This is a experimental observation that cohomology can add nicely when fusing manifolds together in a 'correct' way. The attempt is to ignore the traditional set-up of Mayer-Vietoris and look for a situation, where cohomology adds nicely. This can very conveniently be done in a finite frame work of abstract finite simplicial complexes which come with a natural topology and cohomology reduces to linear algebra. Looking at the topology is really crucial now as we look at open sets in simplicial complexes. We can now look at manifolds which have a closed boundary part (this is the beginning or entry part of the manifold) and an open boundary part (the end or exit part). When gluing such manifolds together, there is no awkward overlap which can carry cohomology stuff llke in Mayer-Vietoris. We get now nice additivity which I call the "fusion formula". If we fuse together the manifolds, the harmonic forms from both sides can settle in the bigger home (just apply the heat flow) and are still present. So, cohomology simply adds. This video is simply an experimental announcement. Things work also for cohomology coming from higher characteristics (and the proof is the same by just applying the heat flow in the fused situation). There are more situation which work like gluing an open Moebius strip (b=(0,0,0)) to a closed disk b=(1,0,0)). A situation which not possible is gluing a closed Moebius strip (b=(1,1,0)) to an open disk b=(0,0,1). The harmonic 2-form present in the open disk can not settle in the union which is a projective plane). I look at a one-dimensional and two-dimensional examples. Examples of spaces with trivial cohomology are half open cylinders. These can be d-spheres in which an open disk has been taken off (stealing the d-form) and a closed disk has been taken off (stealing the 0-form).
[Update 1/30/2023 : just looked at the example of a 3-sphere b=(1,0,0,1) in which a solid torus is cut
away with (this is a 3 manifold with 2-torus boundary) and has b=(1,1,0,0) as it is homotopic to a circle. But the 3-sphere with open 2-torus boundary has b=(0, 1, 0, 1). The fusion formula would suggest (1,2,0,1) which does not match the b=(1,0,0,1) of the 3-sphere. There are more conditions which need to be satisfied to have the fusion formula work. In this example, the 1-form on the torus somehow collides with the 1-form of the complement and both melt away under heat flow in the full 3-sphere. ]
[Update 1/30/2023 : just looked at the example of a 3-sphere b=(1,0,0,1) in which a solid torus is cut
away with (this is a 3 manifold with 2-torus boundary) and has b=(1,1,0,0) as it is homotopic to a circle. But the 3-sphere with open 2-torus boundary has b=(0, 1, 0, 1). The fusion formula would suggest (1,2,0,1) which does not match the b=(1,0,0,1) of the 3-sphere. There are more conditions which need to be satisfied to have the fusion formula work. In this example, the 1-form on the torus somehow collides with the 1-form of the complement and both melt away under heat flow in the full 3-sphere. ]
 0:09:23
0:09:23
 0:17:03
0:17:03
 0:16:20
0:16:20
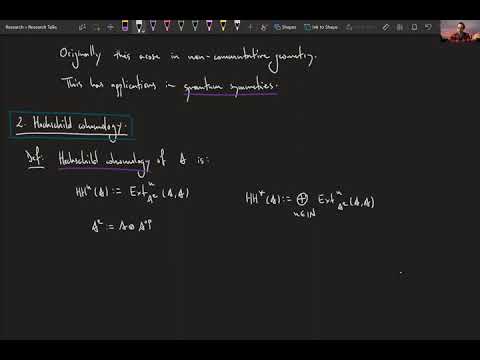 1:20:09
1:20:09
 0:56:50
0:56:50
 0:48:59
0:48:59
 0:11:34
0:11:34
 1:01:40
1:01:40
 0:40:40
0:40:40
 0:59:16
0:59:16
 0:45:27
0:45:27
 0:50:16
0:50:16
 1:07:15
1:07:15
 1:54:09
1:54:09
 0:39:49
0:39:49
 1:36:50
1:36:50
 0:25:13
0:25:13
 0:55:57
0:55:57
 0:45:49
0:45:49
 1:04:21
1:04:21
 1:05:22
1:05:22
 0:11:46
0:11:46
 1:03:14
1:03:14
 1:12:21
1:12:21