Relative extrema, critical numbers, and Fermat's Theorem

preview_player
Показать описание
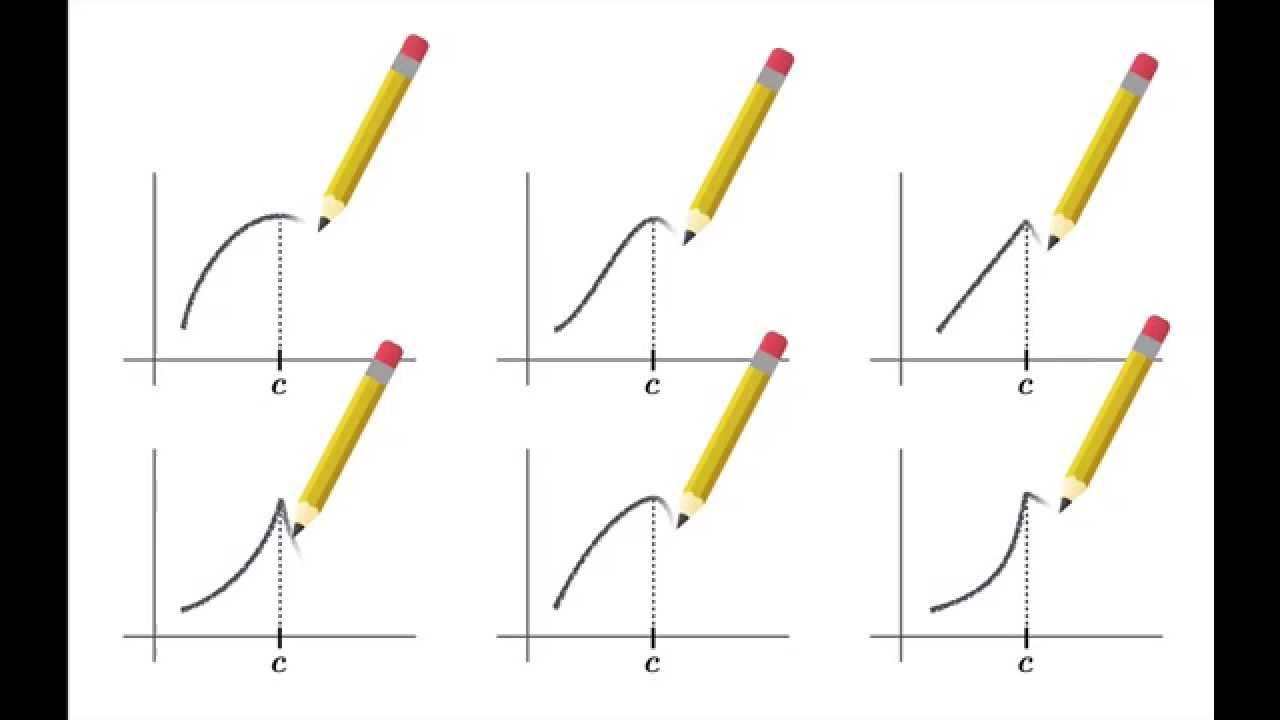
Introduction to the notion of critical numbers of a function (i.e., arguments at which the derivative of the function is either zero or undefined) and Fermat's Theorem, which asserts that relative extrema always occur at a critical number. The video includes a calculation of the critical numbers of f(x) = x^(2/3)(x-2).
  1. Chris Odden
  2. critical numbers
  3. relative extreme
  4. fermat's theorem
  5. calculus
Рекомендации по теме
Finding Critical Numbers 0:21:19

Finding Critical Numbers

Critical Number and 0:02:30

Critical Number and Relative Extrema

Finding Absolute Maximum 0:17:17

Finding Absolute Maximum and Minimum Values - Absolute Extrema

How to Find 0:01:57

How to Find the Critical Numbers and Relative Extrema from the Graph in Calculus

Critical Numbers and 0:01:39

Critical Numbers and Relative Extrema from Graph Simple Example

Local Extrema, Critical 0:14:35

Local Extrema, Critical Points, & Saddle Points of Multivariable Functions - Calculus 3

Critical points introduction 0:07:53

Critical points introduction | AP Calculus AB | Khan Academy

Finding Local Maximum 0:14:18

Finding Local Maximum and Minimum Values of a Function - Relative Extrema

4.1.4 Relative Extrema 0:02:23

4.1.4 Relative Extrema and Critical Numbers

3.1.2 Relative Max 0:14:23

3.1.2 Relative Max & Relative Min - Critical Numbers and Critical Points

Definitions of Extrema 0:13:38

Definitions of Extrema - Relative Extrema - Critical Number

Concept of critical 0:17:21

Concept of critical numbers absolute extrema and relative extrema

Determine the Critical 0:06:05

Determine the Critical Number and Relative Extrema of a Quadratic Function

Absolute and Relative 0:16:00

Absolute and Relative Extrema and the Critical Points

Notes on Relative 0:09:05

Notes on Relative Extrema Part 1 Finding Critical Points

Relative extrema, critical 0:14:52

Relative extrema, critical numbers, and Fermat's Theorem

Finding critical numbers,relative 0:05:41

Finding critical numbers,relative extrema and increasing or decreasing Intervals (Part 1)

Critical Points And 0:08:09

Critical Points And Extrema Definitions

Critical Points, Relative 0:24:12

Critical Points, Relative Maximum & Minimum Values (Extrema)

Extrema and critical 0:14:25

Extrema and critical numbers

Relative Extrema and 0:08:15

Relative Extrema and Critical Numbers

Calculus AB/BC – 0:14:50

Calculus AB/BC – 5.2 Extreme Value Theorem, Global Versus Local Extrema, and Critical Points

Relative Extrema and 0:08:25

Relative Extrema and Critical Numbers

Relative Extrema and 0:11:41

Relative Extrema and Critical Numbers

Комментарии
Автор

at 4:05 you make the claim that the average rate of change between x and c can be <= 0. This does make sense to me since that would only work if x = c which is undefined. Shouldn't it be only be strictly less than? Is there a flaw in my logic?

theflaggeddragon