Composition with Scalars, Vectors, Matrices, and Tensors

by Chan Chak Hang (b.1997)

In music, the pitch class notation is used to represent the 12 pitches in the chromatic scale. It assigns a number to each pitch class, with C being 0, C# being 1, and so on, up to B being 11. For example, the pitch classes in a tone row can be represented as [0, 1, 2, 3, 5, 4, 6, 7, 8, 9, 10, 11]. This notation is useful because it allows us to work with the pitches in a way with mathematic operations.

In addition to serialism, I also work with sets and collections of objects, as well as arithmetic operations. I use PyTorch to assist in my composition process, as it provides easy-to-use operations for tensors or arrays. An array is a collection of elements or values that are organized in a specific order and can be accessed by their index or position. In the context in music composition, arrays are used to represent pitch classes in music and can be constructed in different dimensions, including 0-dimensional (0-D) scalars, 1-D vectors, 2-D matrices, and n-D tensors (n greater than 2). These mathematical concepts of Linear Algebra can be used in music composition to arrange pitch class elements. Scalars are single numbers, vectors are arrays of numbers, matrices are two-dimensional arrays of numbers, and tensors are multi-dimensional arrays of numbers. They can be used to represent complex textures or grouping of motives.

Scalars are single numbers. In music composition, they can be used to transpose pitch classes by a certain number of semitones or multiple each elements in a vector, matrix or tensor. All pitch classes are modulated at 12 (mod 12) if any pitch is greater than 11 after an operation. For example, 12 = 0, 13 = 1 etc.

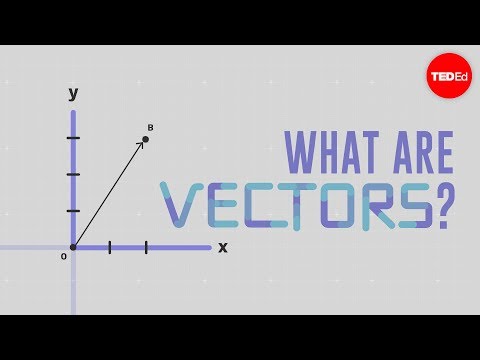
Vectors are one-dimensional arrays of numbers. They can be used to represent a set of pitch classes or notes. For example, a vector can be used to represent a tone row in a monophonic texture.

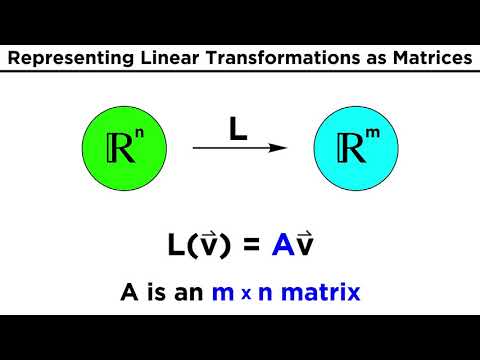
Matrices are two-dimensional arrays of numbers. They can be used to represent operations on vectors or other matrices. For example, a matrix can be used to represent a polyphonic or counterpoint texture.

Tensors are multi-dimensional arrays of numbers. They can be used to represent complex grouping on matrices or other tensors. In music composition, they can be used to represent complex textures or grouping of motives.

Please refer to the link for more details.

#serialism #set_theory #linearalgebra