Two masses and heavy pulley Atwood machine: final velocity and percent energy in each mass.

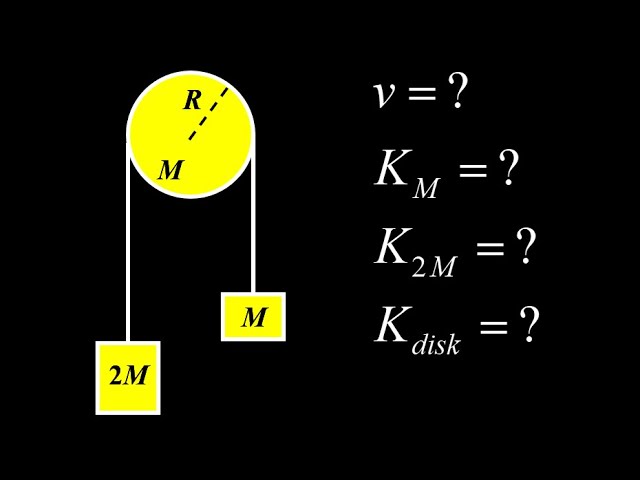
00:00 In this problem, we are given two masses M and 2M and a heavy disk pulley of mass M and radius R to form a two masses and heavy pulley Atwood machine. Final velocity and percent energy in each mass (including the percent energy in the disk) are calculated for the final state of the mass and pulley system after evolving through a distance of d.

00:44 Apply energy conservation to the Atwood machine: we set up the equation for conservation of energy: E_i=E_f. We carefully define the vertical coordinate for each hanging mass so that the initial potential energy of the larger mass is positive and the final potential energy is zero, and for the lighter mass the initial potential energy is zero and the final is positive. Because the mass and pulley system is released from rest, the initial kinetic energy is zero. So we have one potential energy term in the initial state, one potential energy term and three kinetic energy terms in the final state: one for the larger mass moving downward, one for the smaller mass moving upward, and one kinetic energy for the rotating heavy disk pulley in the final state of the system.

02:22 Relating linear and angular velocity for the disk: each mass is moving with a speed of v in the final state, and this is the same as the speed of the string that binds them together. In addition, the string is not slipping on the outside of the disk, so the tangential speed at the edge of the disk is also v. Now we can apply the relation between tangential speed and angular speed v=r*omega to relate angular and linear speed. In the kinetic energy term for the rotating disk, we find an r^2*omega^2, which can now be written as v^2, and we can solve for the final velocity of the masses, v.

04:07 Percent kinetic energy in each mass: now that we have the final velocity of the system, we can compute the percentage of kinetic energy in each moving piece of the system: the two masses moving translationally and the disk moving rotationally. We start by revisiting the energy conservation equation, and we find a compact way of representing the total kinetic energy of the heavy pulley Atwood machine as Mgd. In addition, we have already written out the kinetic energy of each moving component within the energy conservation equation. All we have to do is sub in our expression for the final velocity in terms of g and d, and we have each component of the total kinetic energy expressed as a multiple of the total kinetic energy Mgd. We convert these multiples to percentages, and we're done!