filmov
tv
Differential Equations | Series solution for a second order linear differential equation.

Показать описание
We find a series solution for a second order linear differential equation.
Power Series Solution for a differential equation
Solving Differential Equations with Power Series
How to solve ODEs with infinite series | Intro & Easiest Example: y'=y
POWER SERIES SOLUTION TO DIFFERENTIAL EQUATION
Power Series Solutions to Differential Equations - Series Method for Solving Differential Equations
Differential Equations | Series solution for a second order linear differential equation.
Power Series Solutions of Differential Equations
When can you use Series to solve ODEs? Ordinary vs Singular Points
How to solve differential equations
How to use SERIES to solve DIFFERENTIAL EQUATIONS example: Airy's Equation y''-xy=0
Example of a series solution of a differential equation
Series solution of a differential equation | Lecture 36 | Differential Equations for Engineers
Series Solution Differential Equations (Example 2)
Power Series Solutions of Differential Equations, Ex 2
Power Series Method | Numerical | Series Solution of Differential Equation | Maths
Introduction to series solutions to differential equations (part 1)
Find Two Power Series Solutions for the Differential Equation y'' + xy = 0
PYQs on Power Series Solution in ODE | GATE 1996 to 2023 | Short Cut Tricks
Solving ODEs by the Power Series Solution Method
Power Series - Series Method for Solving Differential Equations - Part 2
Power Series Solution of Bessel's Equation
Differential Equation Power Series Solution for second order
Series Solutions Differential Equations y'' - y' = 0
ODE :: xy'' + y' +2xy = 0 :: Method of Frobenius Series Solution about a Regular Sin...
Комментарии
 0:21:20
0:21:20
 0:18:29
0:18:29
 0:11:01
0:11:01
 0:37:54
0:37:54
 0:18:30
0:18:30
 0:18:09
0:18:09
 0:11:45
0:11:45
 0:08:22
0:08:22
 0:00:46
0:00:46
 0:13:17
0:13:17
 0:18:54
0:18:54
 0:17:19
0:17:19
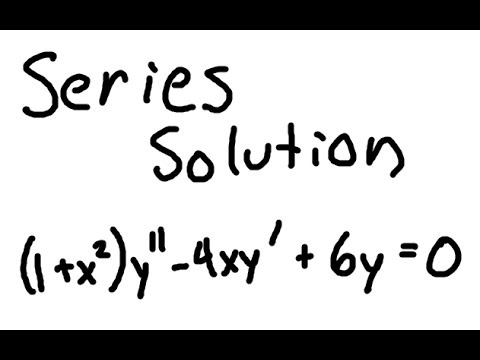 0:30:45
0:30:45
 0:17:01
0:17:01
 0:12:32
0:12:32
 0:22:59
0:22:59
 0:19:45
0:19:45
 0:49:59
0:49:59
 0:11:05
0:11:05
 0:17:35
0:17:35
 0:29:39
0:29:39
 0:18:54
0:18:54
 0:12:59
0:12:59
 0:18:46
0:18:46