Groups: Order of an element divides the order of the group

preview_player
Показать описание
An application of Lagrange's theorem
  1. Adam Glesser
  2. Group-theory
  3. Lagrange
Рекомендации по теме
The Order of 0:03:01

The Order of an Element (Abstract Algebra)

6. Order of 0:15:04

6. Order of an element of a group || Examples || Group Theory #orderofelements

Group Theory 6, 0:13:51

Group Theory 6, order of a Group, order of an element

PART- 2 : 0:17:14

PART- 2 : ORDER OF AN ELEMENT IN A GROUP | ALGEBRAIC STRUCTURES | DISCRETE MATHEMATICS

Groups: Order of 0:02:57

Groups: Order of an element divides the order of the group

Order of an 0:04:07

Order of an Element Divides the order of a finite cyclic group Proof (Abstract Algebra)

PART-1: ORDER OF 0:27:31

PART-1: ORDER OF AN ELEMENT IN A GROUP | ALGEBRAIC STRUCTURES | DISCRETE MATHEMATICS

Order Of an 0:02:55

Order Of an Element of a Group | Order | Abstract algebra | Group Theory|

3.Order of a 0:20:43

3.Order of a group | Order of an element | Fully Concept Explained | Must watch

Corollary |a| Divides 0:03:46

Corollary |a| Divides |G|, the order of each element of the group divides the order of the group.

Abstract Algebra 8.2: 0:06:43

Abstract Algebra 8.2: Order of an Element in a Direct Product

order of an 0:02:12

order of an element in Quotient group theory additive abstract algebra IIT Jam 2012 mathematics

The order of 0:05:22

The order of an element of a group is the same as that of its inverse a^-1

order of an 0:05:04

order of an element in Quotient group theory abstract algebra iit jam 2012 mathematics how to find

order of an 0:03:02

order of an element in a quotient group theory additive abstract algebra IIT Jam 2012 mathematics

order of an 0:04:14

order of an element in permutation group order of permutation group sigma symmetric group s7

Group Theory| Lecture 0:36:36

Group Theory| Lecture 41| Order of an element of a group| Examples| Theta Classes

number of element 0:00:38

number of element of order 2 in Dn group theory abstract algebra modern algebra

Group Theory, Lec_19, 0:43:05

Group Theory, Lec_19, Order of group and order of an element in a group. B.Sc.(ADP),B.S/M.Sc. Math

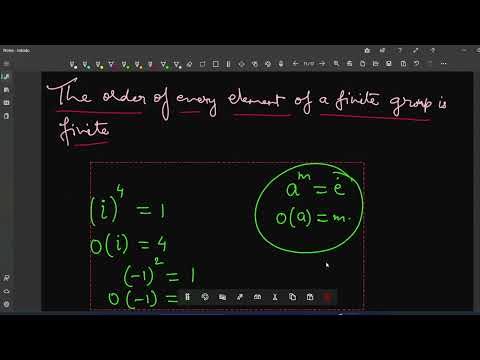
The order of 0:09:44

The order of every element of a finite group is finite

Exponents and the 0:05:53

Exponents and the Order of a Group Element

Find Order of 0:05:14

Find Order of an Element when Binary operation is Addition With Examples Abstract Algebra

lec#21 order of 0:12:19

lec#21 order of an element of a group under addition (group theory)

Order of an 0:00:44

Order of an element of a Group Lecture#22

Комментарии
Автор

Oh, it's rather quite simple but it has eluded me all day. Thanks a lot, that makes sense.

aiiishiba
Автор

So, typically, the element x will not generate the entire group G. However, x will always generate the subgroup (x) = {x^i | i an integer}, and the order of x equals the order of (x). By Lagrange's theorem the order of (x) divides the order of G, and so the order of x must divide the order of G.

AdamGlesser
Автор

Dude you're a G, this helped me out so much fam

lilhonky
Автор

Thanks a lot for all the lectures on Math especially on " COMPLEX ANALYSIS " . Can you please upload a lecture series on " GROUP THEORY " .
Again Lots and lots and lots of thanks .

tawabullas
Автор

What if the element doesn't generate the group, how do you prove it divides the element of the group.

aiiishiba
Автор

I would love to, and in the future might. First, I need to get a grant!

AdamGlesser