filmov
tv
Neural Networks from Scratch - P.9 Introducing Optimization and derivatives

Показать описание
Introducing the challenge of optimization and the concepts of derivatives
#deeplearning #machinelearning #nnfs
#deeplearning #machinelearning #nnfs
I Built a Neural Network from Scratch
Building a neural network FROM SCRATCH (no Tensorflow/Pytorch, just numpy & math)
But what is a neural network? | Chapter 1, Deep learning
Neural Network from Scratch | Mathematics & Python Code
Neural Networks from Scratch - P.1 Intro and Neuron Code
How to Create a Neural Network (and Train it to Identify Doodles)
Neural Networks Explained from Scratch using Python
Create a Simple Neural Network in Python from Scratch
Convolution Neural Network Step By Step Implementation | Tutorial | Deep Learning With Image data
Understanding AI from Scratch – Neural Networks Course
Neural Network From Scratch In Python
Neural Networks from Scratch - P.5 Hidden Layer Activation Functions
Neural Networks from Scratch - P.4 Batches, Layers, and Objects
Neural Network from scratch using Only NUMPY
Convolutional Neural Network from Scratch | Mathematics & Python Code
Creating a Neural Network from scratch in under 10 minutes
How to train simple AIs
Neural Networks from Scratch - P.6 Softmax Activation
The Complete Mathematics of Neural Networks and Deep Learning
Running a NEURAL NETWORK in SCRATCH (Block-Based Coding)
Lecture 1 - Neural Network from Scratch: Coding Neurons and Layers
Neural Networks from Scratch announcement
Neural Networks from Scratch - P.2 Coding a Layer
Neural Networks From Scratch in Rust
Комментарии
 0:09:15
0:09:15
 0:31:28
0:31:28
 0:18:40
0:18:40
 0:32:32
0:32:32
 0:16:59
0:16:59
 0:54:51
0:54:51
 0:17:38
0:17:38
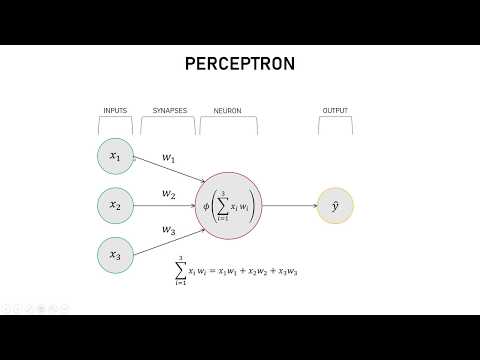 0:14:15
0:14:15
 0:42:12
0:42:12
 3:44:18
3:44:18
 1:13:07
1:13:07
 0:40:06
0:40:06
 0:33:47
0:33:47
 1:39:10
1:39:10
 0:33:23
0:33:23
 0:10:41
0:10:41
 0:12:59
0:12:59
 0:34:01
0:34:01
 5:00:53
5:00:53
 0:13:29
0:13:29
 0:28:37
0:28:37
 0:11:35
0:11:35
 0:15:06
0:15:06
 0:09:12
0:09:12