filmov
tv
Solving Systems of Linear Equations in Three Variables

Показать описание
In this lesson, we will review how to solve a system of linear equations in three variables. Although we can use substitution for this type of problem, we will use an extension of the elimination method. First, we will make sure each equation is written in the format of: ax + by + cz = d. Basically, all the variable terms need to be on one side and the constant needs to be on the other. Now, we want to pick a variable to eliminate, it can be x, y, or z. We will choose any two equations and eliminate this variable by transforming both equations in such a way that one pair of variable terms are opposites. Once this is done, we can add the left sides and set this equal to the sum of the right sides. Now we will have a linear equation with only two variables. Next, we will choose two different equations, and eliminate the same variable. This will now give us two equations with two variables. We can solve this system using substitution, or elimination, depending on what is preferred for that given system. Once this is done, we can substitute back into one of the original equations in order to obtain the final unknown. Additionally, we will cover special case scenarios. These occur when we have no solution, or infinitely many solutions. If in the process of solving our system, we end up with a false statement, we can stop and state that our answer is "no solution". If in the process of solving our system, we end up with a statement that is always true, we can stop and state that our answer is "infinitely many solutions".
Комментарии
 0:10:27
0:10:27
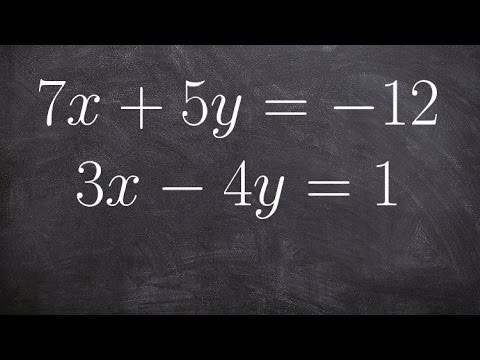 0:04:34
0:04:34
 0:05:15
0:05:15
 0:10:52
0:10:52
 0:10:21
0:10:21
 0:12:28
0:12:28
 0:18:40
0:18:40
 0:12:44
0:12:44
 1:03:45
1:03:45
 0:05:59
0:05:59
 0:12:16
0:12:16
 0:12:44
0:12:44
 0:09:21
0:09:21
 0:17:32
0:17:32
 0:05:03
0:05:03
 0:19:44
0:19:44
 0:18:18
0:18:18
 0:09:55
0:09:55
 0:04:49
0:04:49
 0:05:42
0:05:42
 0:10:47
0:10:47
 0:10:45
0:10:45
 0:15:55
0:15:55
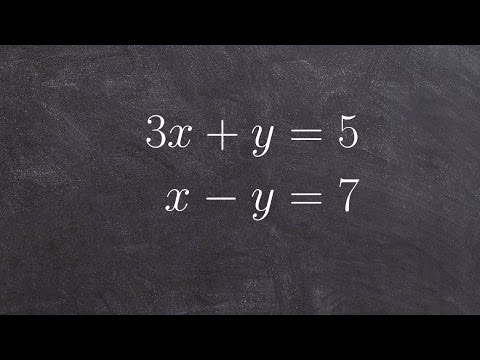 0:05:22
0:05:22