filmov
tv
Machine Learning course- Shai Ben-David: Lecture 8

Показать описание
CS 485/685, University of Waterloo. Jan 30, 2015.
The relationship of VC dimension and learning: Statement of the "fundamental theorem of statistical machine learning" and a proof of the non-learnability of classes of infinite VC-dimension.
The relationship of VC dimension and learning: Statement of the "fundamental theorem of statistical machine learning" and a proof of the non-learnability of classes of infinite VC-dimension.
Machine Learning course- Shai Ben-David: Lecture 1
Machine Learning course- Shai Ben-David: Lecture 2
A short introduction to infinite sets
Machine Learning course- Shai Ben-David: Lecture 21
Machine Learning course- Shai Ben-David: Lecture 22
Machine Learning course- Shai Ben-David: Lecture 12
Machine Learning course- Shai Ben-David: Lecture 18
Machine Learning course - Shai Ben-David : Lecture 5 by Mohammad-Hassan Zokaei Ashtiani
Machine Learning course- Shai Ben-David: Lecture 16
Machine Learning course- Shai Ben-David: Lecture 14
Machine Learning course- Shai Ben-David: Lecture 3
Dr. Shai Ben-David talking about CS485, Foundations of Machine Learning.
Learning probability distributions; What can, What can't be done - Shai Ben-David
Machine Learning course- Shai Ben-David: Lecture 7
Machine Learning course- Shai Ben-David: Lecture 8
Machine Learning course- Shai Ben-David: Lecture 4
Machine Learning course- Shai Ben-David: Lecture 13
Unprovability and Other Impossibility Results in Machine Learning
Machine Learning course- Shai Ben-David: Lecture 17
Machine Learning course- Shai Ben-David: Lecture 23
Machine Learning course- Shai Ben-David: Lecture 11
Shai Ben-David on 'How Far Are We From Having a Satisfactory Theory of Clustering?'
Machine Learning course- Shai Ben-David: Lecture 20
Machine Learning course- Shai Ben-David: Lecture 15
Комментарии
 1:18:12
1:18:12
 1:17:51
1:17:51
 0:52:51
0:52:51
 1:18:58
1:18:58
 1:08:24
1:08:24
 1:16:29
1:16:29
 1:18:58
1:18:58
 1:16:36
1:16:36
 1:16:21
1:16:21
 1:18:31
1:18:31
 1:17:58
1:17:58
 0:05:48
0:05:48
 0:57:09
0:57:09
 1:18:33
1:18:33
 1:19:53
1:19:53
 1:18:48
1:18:48
 1:20:09
1:20:09
 0:46:56
0:46:56
 1:17:37
1:17:37
 1:21:02
1:21:02
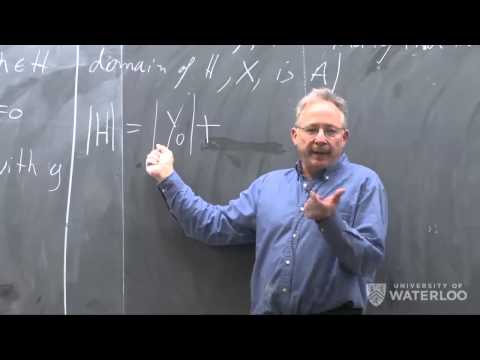 1:19:40
1:19:40
 0:54:40
0:54:40
 1:15:06
1:15:06
 1:18:59
1:18:59