filmov
tv
super square root of 256 = ?

Показать описание
Solving x^2=2^x by using the super square root:
------------------------------------------------------------------------------------
bprp #fast
------------------------------------------------------------------------------------
bprp #fast
super square root of 256 = ?
Square Root 256
Simplify sqrt(-256)
Super square root of number
find the sqrt of 256 to the 3rd⁰ in 3 quick steps #mathstricks
What is the square root of 256?
raiz cuadrada de - 256 , raiz cuadrada de menos , square root of - 256
Derivative of the super square root
What is the square root of 256?
SQUARE ROOT OF 256
resolución de una raíz de 256 elevado a un índice 8.
solving x^2=2^x with the super square root
A super fast math trick for nested square roots
Super fast trick for finite series under square root || Type √x√x√x√x=x^y
Find the square root of 256? - QnA Explained
Square root of 256 l Prime Factorization Method
9√256 , 9 Por Raiz cuadrada de 256 , raiz por un numero , multiplicacion
#super Square Root Trick........#short #shortsvideo
Find the square root of a number in BASIC 256 | Calculate the square root of number
FIND THE VALUE OF BASE ROOT 2 POWER 256 #Sahasragade
Short Tricks on Square Root in 5 Seconds | How to find Square Root | #shorts #short #shortvideo
#MATHS TRICK OF FINDING #SQUARE MORE THAN 100 - #tricks #shorts
Raiz cuadrada de 256 , metodo de descomposicion , descomponiendo , proceso mcm
10√256 , 10 Por Raiz cuadrada de 256 , raiz por un numero , multiplicacion
Комментарии
 0:00:48
0:00:48
 0:01:09
0:01:09
 0:01:29
0:01:29
 0:00:26
0:00:26
 0:01:49
0:01:49
 0:03:16
0:03:16
 0:01:03
0:01:03
 0:01:19
0:01:19
 0:05:58
0:05:58
 0:02:56
0:02:56
 0:00:16
0:00:16
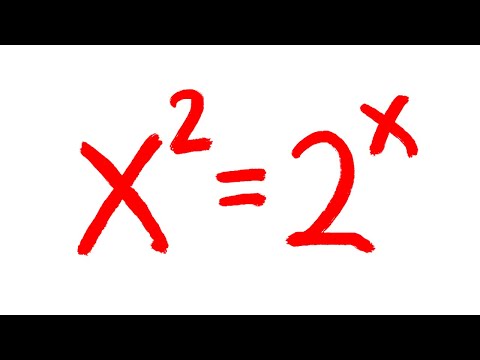 0:09:10
0:09:10
 0:00:20
0:00:20
 0:00:14
0:00:14
 0:01:37
0:01:37
 0:02:14
0:02:14
 0:00:54
0:00:54
 0:00:47
0:00:47
 0:01:39
0:01:39
 0:01:07
0:01:07
 0:00:50
0:00:50
 0:00:28
0:00:28
 0:02:06
0:02:06
 0:00:49
0:00:49