3.1.2 Laplace's Equation in 1D

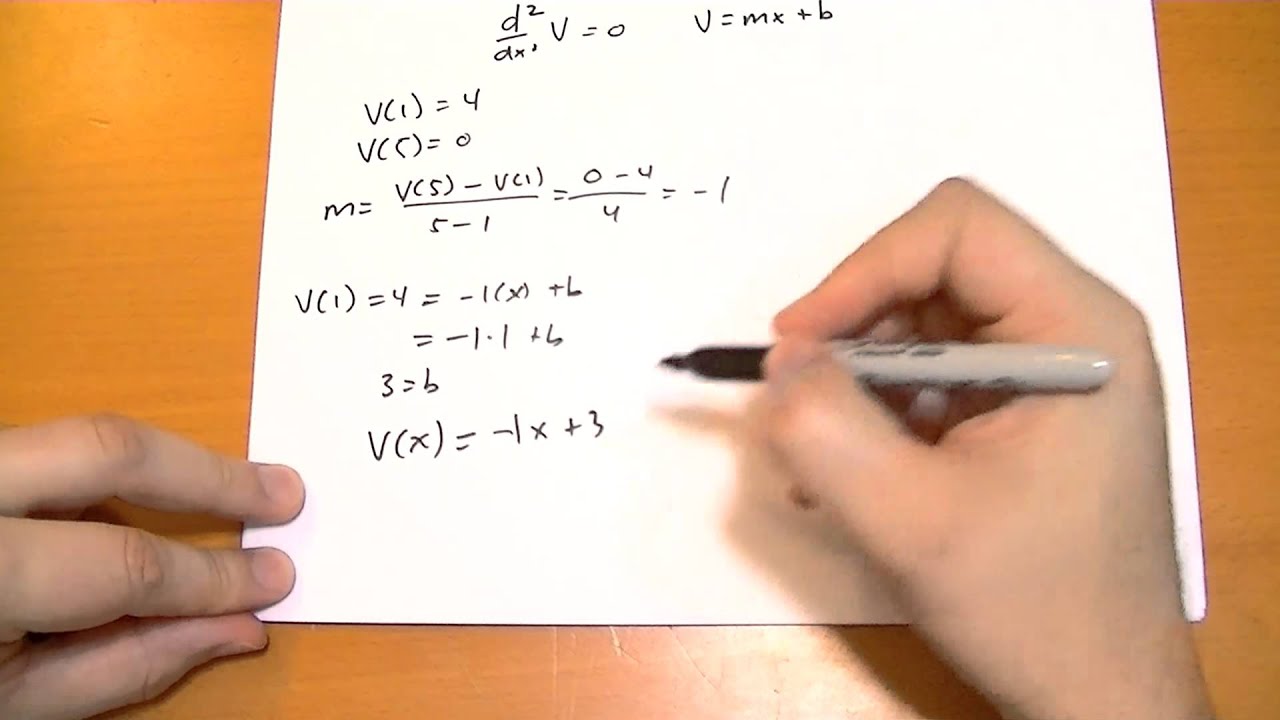
preview_player
Показать описание
Laplace's Equation in one dimension is rather trivial, but two rules will help us better understand what it looks like in 2 and 3 dimensions.

  1. Real Physics
  2. physics
  3. Laplace's Equation
  4. electrostatics
Рекомендации по теме
3.1.2 Laplace's Equation 0:04:05

3.1.2 Laplace's Equation in 1D

Solving the Laplace 0:06:45

Solving the Laplace Equation in 1D

3.1.1 Introduction to 0:04:15

3.1.1 Introduction to Laplace's Equation

Poisson's Equation and 0:09:59

Poisson's Equation and Laplace's Equation

Laplacian intuition 0:05:31

Laplacian intuition

3.1.4 Laplace's Equation 0:09:57

3.1.4 Laplace's Equation in 3D

BEST DEFENCE ACADEMY 0:00:15

BEST DEFENCE ACADEMY IN DEHRADUN | NDA FOUNDATION COURSE AFTER 10TH | NDA COACHING #shorts #nda #ssb

3.1.3 Laplace's Equation 0:03:44

3.1.3 Laplace's Equation in 2D

Lecture 34-Electrostatics -II: 0:28:13

Lecture 34-Electrostatics -II: Solving Laplace's equation in 1D

Laplace transforms | 3:19:27

Laplace transforms | Series Solutions | System of ODEs | Differential Equations | Review 3

Differential Equations: Laplace 0:59:51

Differential Equations: Laplace Transformations, 10-31-17, part 1

Solving the heat 0:14:13

Solving the heat equation | DE3

Logical Reasoning???#viral #vidumzn 0:00:11

Logical Reasoning???#viral #vidumzn

PDE: Heat Equation 0:21:17

PDE: Heat Equation - Separation of Variables

Derivation and Solution 0:33:40

Derivation and Solution of Laplace’s Equation

Isaac Newton's INSANE 0:00:24

Isaac Newton's INSANE Sleep Habits 😬

(11). Find the 0:02:42

(11). Find the Laplace Transform of x^2(e^-3x) in MSC Mathematics Semester-1

Laplace equation 0:16:46

Laplace equation

Using Laplace Transforms 0:11:50

Using Laplace Transforms to Solve Differential Equations

Beauty of the 0:00:19

Beauty of the Brain😍 IQ - IIT Bombay

Cosplay by b.tech 0:00:15

Cosplay by b.tech final year at IIT Kharagpur

Solving heat equation 0:49:15

Solving heat equation by Laplace transform

That's Why Mohit 0:00:19

That's Why Mohit Sir Called 'God Of Mathematics'| Puzzle Brain teaser | #competishun ...

Heat equation problem 0:05:22

Heat equation problem (inverse Laplace) RMM problem

Комментарии
Автор

These videos are awesome man. I'm taking this class now and this has definitely helped.

GLXLR
Автор

I should've said, "The actual value for b is left as an exercise for the viewer."

jg
Автор

That's a GREAT question and the answer is that sin(ax) is not a solution in 1D. The reason is quite simple. Laplace's equation says that the 2nd derivative has to be 0 everywhere. The 2nd derivative of sin is not 0 everywhere. In 2 and 3 dimensions, the SUM of the 2nd derivatives have to be zero everywhere, and so you can have solutions like sin and e as long a the 2nd derivatives cancel each other out at all points.

jg
Автор

Sir i didnt get that average part 1st point you have written ca you explain please?

josephksajan
Автор

Doubt: If the first derivative is 0 how is there a value of the second derivative??

ayushkharwar
Автор

You know whats best about you?
You dont just read the words of griffiths book like all the other so called teachers online. You explain it in simple words

info-hub
Автор

U r just reading out the book...stop it

AnilKumar-byzi