filmov
tv
HOW TO FIND EQUATION OF TANGENT LINE WITH IMPLICIT DIFFERENTIATION

Показать описание
In order to find the equation of a tangent line to a given function at a given point, you need to consider what a tangent line is. In order for a line to be considered a tangent line you need to make sure that 2 conditions are met:
1. The line needs to go through the given point.
2. The line needs to have the same slope as the given function at that shared point.
In this video I'll show you how to find the equation of a tangent line to the function 16x^2+y^2=xy+4 at the point (0, 2). This means that we will be coming up with a linear function that goes through the point that lies on the function at (0, 2) and has the same slope as 16x^2+y^2=xy+4 at that point. We will come up with this tangent line equation with the derivative of our given function.
READ MORE
WATCH NEXT
YOU MIGHT ALSO BE INTERESTED IN...
Some links in this description may be affiliate links meaning I would get a small commission for your purchase at no additional cost to you.
1. The line needs to go through the given point.
2. The line needs to have the same slope as the given function at that shared point.
In this video I'll show you how to find the equation of a tangent line to the function 16x^2+y^2=xy+4 at the point (0, 2). This means that we will be coming up with a linear function that goes through the point that lies on the function at (0, 2) and has the same slope as 16x^2+y^2=xy+4 at that point. We will come up with this tangent line equation with the derivative of our given function.
READ MORE
WATCH NEXT
YOU MIGHT ALSO BE INTERESTED IN...
Some links in this description may be affiliate links meaning I would get a small commission for your purchase at no additional cost to you.
How To Find The Equation of a Line From a Graph | Algebra
GCSE Maths - How to Find the Equation of a Straight Line (y = mx + c) #68
How To Find The Equation of a Line Given Two Points
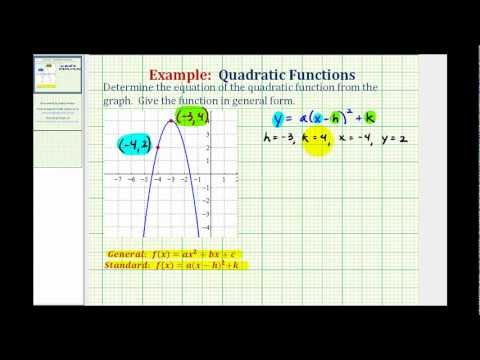
How To Find The Equation of a Quadratic Function From a Graph
How to find the equation of a line given two points
Finding the equation of a straight line given the gradient and a point
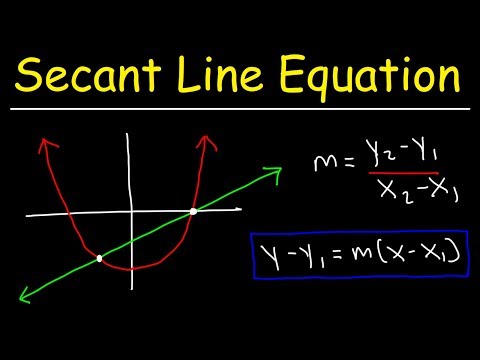
How To Find The Equation of a Secant Line
NECO 2020 Question 30 | Equation of a straight line
Find Equation of Line Perpendicular to a Line Through a Given Point
Find the equation of a line through two points using slope intercept form
How To Find The Equation of the Normal Line
Find The Equation of A Line Given Two Points - Understand In 10 Minutes
GCSE Maths - Finding the Equation of a Straight Line From 2 Sets of Coordinates #69
How To Find The Equation of a Plane Given Three Points
Finding the Equation of a Line in Slope Y-Intercept Form
How To Find The Equation of a Plane Given a Point and Perpendicular Normal Vector
Finding the Equation of a Line Given Slope and a Point - Point - Slope Form
How To Find The Vector Equation of a Line and Symmetric & Parametric Equations
Find the Equation of a Quadratic Function from a Graph (a less than 0)
Ex: Find the Equation of a Quadratic Function from a Graph
Finding the Equation of a Tangent
Finding the Equation of a Polynomial from a Graph
How to find equation of exponential Function from Graph
How To Write The Equation of a Line Given The Slope and a Point | Algebra
Комментарии
 0:10:05
0:10:05
 0:04:28
0:04:28
 0:07:38
0:07:38
 0:09:35
0:09:35
 0:04:41
0:04:41
 0:01:54
0:01:54
 0:05:04
0:05:04
 0:05:52
0:05:52
 0:02:26
0:02:26
 0:05:04
0:05:04
 0:10:25
0:10:25
 0:11:26
0:11:26
 0:06:07
0:06:07
 0:06:56
0:06:56
 0:04:28
0:04:28
 0:07:37
0:07:37
 0:08:28
0:08:28
 0:11:37
0:11:37
 0:04:35
0:04:35
 0:04:56
0:04:56
 0:04:39
0:04:39
 0:04:03
0:04:03
 0:02:39
0:02:39
 0:08:32
0:08:32