Operations Research 09B: Branch and Bound for Integer Programming

Textbooks:

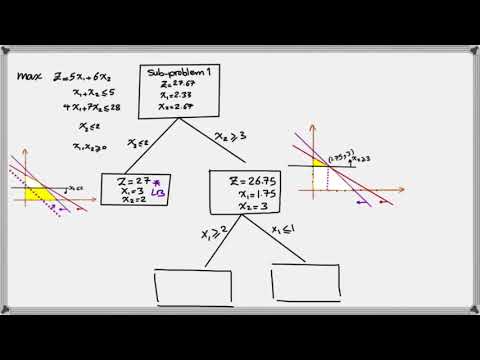
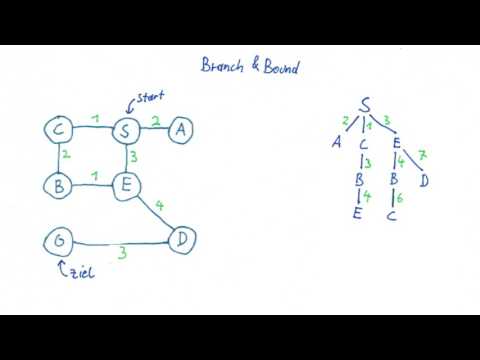
In this video, I'll talk about how to solve IP problems using the branch and bound method. The branch-and-bound algorithm is actually an enumeration of candidate solutions in the search space. It splits the original problem into branches of subproblems.
Before enumerating the candidate solutions of a branch, the branch is checked against upper or lower estimated bounds of the optimal solution. The branch is discarded if it cannot produce a better solution than the best one found so far by the algorithm.

----------------------------------------

[YongWang]

Hi Guys, please comment and let me know what you think about this Operations Research Open Course. Your feedback is really appreciated. If you enjoy the video, please subscribe and share. All my replies here are only related to the content in my own videos. I am afraid I won't be able to answer other questions. Thanks for your understanding.

[haoduan]

Invaluable branch and bound lesson, save me from the hell of the final exam!

[motox]

Great video! Your whole series of videos is helping me study for my 5340 final !

[tabita]

second example , first iteration in x=1 branch, values shod be 1, .8, 0, .8

[iseyunhan]

Hi sir, can you explain for me in 5:57 why you chose the constraint x2<=1 not x2>=2 please?

[aysegulsen]

Thanks to your understandable expression, I understand very well .Thank you. Great video

[World_Admiror]

Thank you for the efforts you put in. I'm so thrilled I watched this video. But in my view, in the first maximization problem example, we are interested in looking for the greatest lower bound. So, I think we should say in 7:20 the lower (instead of upper) bound of this branch 12.17 is worse than the current z* value 13.5. Which makes sense because we ended up with the final optimal solution (13.5) which is actually the greatest lower bound.
If the problem was a minimization problem we would be interested in finding the lowest upper bound.

[preettapreetta]

sir this video is very useful to us, your definition is very clear.

[krumpy]

Hello, I‘m interested in timetabling/schwduling problems, specifically where one tried to find a solution to the problem where for example we have X teachers, Y classes, Z Classrooms and then try to find a an appropriate schedule subject to some constraints like every class is taught twice per week in 1 of 3 school subjects and only one subject per day etc… Can someone help to find resources in these kind of problems?

[mengnixu]

hi thank you. i have a question though. the Z* with the point( 0, 0 2, 0.5) why is it the optimal solution? because 0.5 is still decimal number, not the integer number..
hope to resolve
Thank you

[Galahad]

Should we solve simplex again and again for each branch? Doesn't it make it too long?

[patricioguerra]

I think that the LP RELAXATION answer is wrong, I obtained 17.3 for z and 2.6 for x2
Is that correct?

[bidusikhadka]

Professor Wang, it was really helpful. I have a question though. When both the branches are unfathomed, how do we chose which branch to further expand into? It would have been even better if you would have included a case where while rechecking, a previously unfathomed subproblem was the solution in your second example and if a few real-life examples of applications of each type of IP was mentioned. Yet, this video is informative and gave me a basic idea of the branch and bound. So, thank you, sir.

[abdelrhmanahmed]

you max is wrong it should be 20.25 for lp relaxation and so on for the rest

[minglee]

Branch and bound, branch and cut, branch and price. OMG