filmov
tv
Indian National Mathematics Olympiad 2013 Problem 2
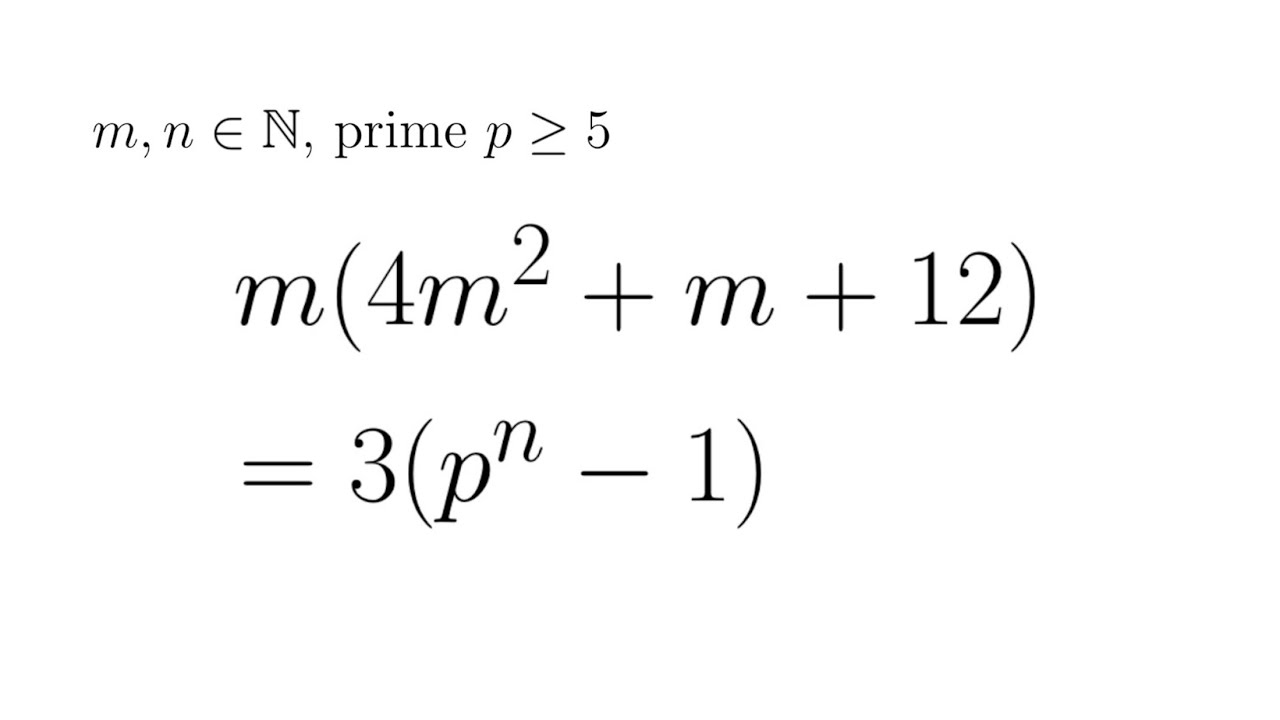
Показать описание
Indian National Mathematics Olympiad 2013 Problem 2
INMO 2013 - Fundamentals of Inequality | Maths Olympiad | Problem 3
Asian Pacific Mathematical Olympiad 2013 Problem 2
🇸🇬 SINGAPORE MATHEMATICAL OLYMPIAD 2013 QUESTION NUMBER - 5
INMO 2013 - Number Theory | Diophantine Equation | Maths Olympiad | Problem 2
Olympiad Question from India
INMO 2013 - Polynomials ( Application of Vieta's Theorem ) | Algebra | Maths Olympiad | Probl...
A Nice and Simple Equation in National Maths Olympiad
INMO 2013 Q1 - INMO Flashback | Math Olympiad Preparation | INMO 2022-23 | Lohit Jindal | VOS
🇸🇬 SINGAPORE MATHEMATICAL OLYMPIAD - 2013, QUESTION NUMBER - 13
🇬🇧 UKRANIAN MATHS OLYMPIAD 2005
A Surprisingly Easy National Maths Olympiad Problem
INMO 2013 | Problem 5 | Olympiad Problem Solving | Math Education
RMO 2013 Problem | PRMO | RMO | MATHS | OLYMPIAD |INMO | IITJEE | Mathematics | Can you solve it !!
INMO 2013 Q3 - INMO Flashback | Math Olympiad Preparation | INMO 2022-23 | Lohit Jindal | VOS
One Simple Trick to Solve This National Maths Olympiad Problem
International Mathematical Olympiad (IMO) 1995 - solutions
Indian Mathematical Olympiad || RMO 2002
Indian Math Olympiad 2023 - Euler's name everywhere!
🇸🇬 SINGAPORE MATHEMATICAL OLYMPIAD 2013 QUESTION NUMBER - 1
Indian Mathematical Olympiad | RMO 2000
Indian Math Olympiad 2014 #2 | A floor problem amenable to experimentation
Online Math Olympiad Preparation
How to solve equations with |X|: From 2020 Indian National Olympiad
Комментарии
 0:11:29
0:11:29
 0:08:44
0:08:44
 0:10:13
0:10:13
 0:02:01
0:02:01
 0:20:33
0:20:33
 0:10:45
0:10:45
 0:11:56
0:11:56
 0:07:41
0:07:41
 0:16:55
0:16:55
 0:01:44
0:01:44
 0:03:12
0:03:12
 0:02:51
0:02:51
 0:18:58
0:18:58
 0:06:40
0:06:40
 0:12:11
0:12:11
 0:06:38
0:06:38
 0:40:44
0:40:44
 0:04:10
0:04:10
 0:13:14
0:13:14
 0:01:57
0:01:57
 0:10:15
0:10:15
 0:14:07
0:14:07
 0:08:39
0:08:39
 0:04:00
0:04:00