filmov
tv
Proving a mapping is linear #python #olympiad #ap calculus#praxis 2#java #python# putnam#amc math#c+

Показать описание
To Define that a mapping is linear. We have to check that the sum of 2 vectors in the space under f is the Sum of that images. That means if we have X and Y in some space E we have f of x plus y equals f of x plus F of Y. And again, we need to make sure that we have any linear combination of these 2 factors the X and Y we can take Alpha and beta in R and we combine Alpha X Plus beta Y and we check the image of alpha of f of x plus beta y equals to Alpha f of x plus beta F of Y. This will help us prove that f is linear we can also make sure that F of 0 is equal to zero.
This will let us know that our mapping or our function is linear. Once we do that we can give a geometric explanation for this linear mapping to do that. We can add 2 vectors and see how they behave when we apply F to them.
We will use more linear mappings when we deal with differentials when we deal with gradients with vectors linear integrals. And also when we deal with linear forms in general, but for now we can use this 1 here on equations. We will use this 1 for differential equations our tangent equations and all in all the equations that we will use for our problem that we will have to solve these equations that are very important like the equation of the line the equation of the circle the equation of the normal the equation of the the tangent and all that. We going to use them by using these linear map. So it's good to know.
#maths #olympiad #python #calculus #java #mathematics #ap #tennis #c
This will let us know that our mapping or our function is linear. Once we do that we can give a geometric explanation for this linear mapping to do that. We can add 2 vectors and see how they behave when we apply F to them.
We will use more linear mappings when we deal with differentials when we deal with gradients with vectors linear integrals. And also when we deal with linear forms in general, but for now we can use this 1 here on equations. We will use this 1 for differential equations our tangent equations and all in all the equations that we will use for our problem that we will have to solve these equations that are very important like the equation of the line the equation of the circle the equation of the normal the equation of the the tangent and all that. We going to use them by using these linear map. So it's good to know.
#maths #olympiad #python #calculus #java #mathematics #ap #tennis #c
 0:07:49
0:07:49
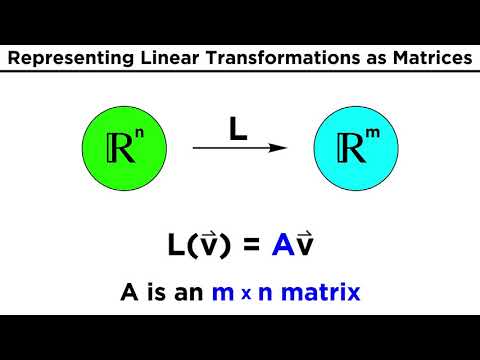 0:09:11
0:09:11
![[Linear Algebra] Dimension](https://i.ytimg.com/vi/Csgbd3n6kmw/hqdefault.jpg) 0:03:14
0:03:14
 0:06:46
0:06:46
 0:10:59
0:10:59
 0:01:01
0:01:01
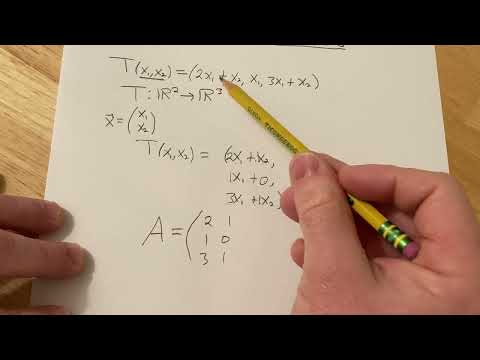 0:05:19
0:05:19
 0:09:06
0:09:06
 0:15:43
0:15:43
 0:06:09
0:06:09
 0:13:52
0:13:52
 0:05:45
0:05:45
 0:00:15
0:00:15
![[Linear Algebra] Vector](https://i.ytimg.com/vi/U5Se4dixU1k/hqdefault.jpg) 0:05:04
0:05:04
 0:08:46
0:08:46
 0:09:20
0:09:20
 0:01:01
0:01:01
![[Linear Algebra] Injective](https://i.ytimg.com/vi/WpUv72Y6Dl0/hqdefault.jpg) 0:16:45
0:16:45
 0:05:35
0:05:35
 0:26:07
0:26:07
 0:06:29
0:06:29
 0:05:04
0:05:04
 0:16:04
0:16:04
 0:10:44
0:10:44