filmov
tv
If f(x) = log((1+x)/(1-x)), then f(2x/(1+x^2 )) is equal to a)〖{f(x)}〗^2 b) 〖{f(x)}〗^3 c) 2f(x)

Показать описание
Function Lecture:
If f(x) = log((1+x)/(1-x)), then f(2x/(1+x^2 )) is equal to
a)〖{f(x)}〗^2 b) 〖{f(x)}〗^3 c) 2f(x) d) 3f(x)
Relations and Functions For Class 12 Concepts
The topics and subtopics covered in relations and Functions for class 12 are:
Introduction
Types of relations
Types of Functions
Composition of functions and invertible functions
Binary operation.
Let us discuss the concept of relation and function in detail
Relation
The concept of relation is used in relating two objects or quantities with each other. If two sets are considered, the relation between them will be established if there is a connection between the elements of two or more non-empty sets.
Types of Relations
A relation in set A is a subset of A × A. Thus, A × A is two extreme relations.
Empty Relation
If no element of A is related to any element of A, i.e. R = φ ⊂ A ×A, then the relation in a set is called empty relation.
Universal Relation
If each element of A is related to every element of A, i.e. R = A × A, then the relation is said to be universal relation.
A relation R in a set A is called-
Reflexive- if (a,a) ∈ R, for every a ∈ A.
Symmetric- if (a1,a2) ∈ R implies that (a2,a1) ∈ R , for all a1,a2∈ A.
Transitive- if (a1,a2) ∈ R and (a2,a3) ∈ R implies that (a1,a3) ∈ R for all a1,a2,a3 ∈ A.
Equivalence Relation- A relation in a set A is equivalence relation if R is reflexive, symmetric and transitive.
Functions
A function is a relationship which explains that there should be only one output for each input. It is a special kind of relation(a set of ordered pairs) which obeys a rule i.e every X-value should be connected to only one y-value.
Types of Functions
One to one Function: A function f : X → Y is defined to be one-one (or injective), if the images of distinct elements of X under f are distinct, i.e., for every x1 , x2 ∈ X, f(x1 ) = f(x2 ) implies x1 = x2 . Otherwise, f is called many-one.
Onto Function: A function f : X → Y is said to be onto (or surjective), if every element of Y is the image of some element of X under f, i.e., for every y ∈ Y, there exists an element x in X such that f(x) = y.
One-one Function: A function f : X → Y is said to be one-one and onto (or bijective), if f is both one-one and onto.
Composition of Functions and Invertible Function
Let f : A → B and g : B → C be two functions. Then the composition of f and g, denoted by gof, is defined as the function gof : A → C given by;
gof (x) = g(f (x)), ∀ x ∈ A
Binary Operations
A binary operation ∗ on a set A is a function ∗ : A × A → A. We denote ∗ (a, b) by a ∗ b.
Example: Show that subtraction and division are not binary operations on R.
Solution: R × R → R, given by (a, b) → a – b, is not binary operation, as the image of (3, 5) under ‘–’ is 3 – 5 = – 2 ∉ R.
Similarly, ÷: R × R → R, given by (a, b) → a ÷ b is not a binary operation, as the image of (3, 5) under ÷ is 3 ÷ 5 = 3 5 ∉ R.
A function : X Y is one-one (or injective), if .
A function : X Y is onto (or surjective), if such that
A function : X Y is one-one-onto (or bijective), if is both one-one and onto.
The composition of function : A B and : B C is the function given by
A function : X Y is invertible, if such that and
A function : X Y is invertible, if and only if is one-one and onto.
Given a finite set X, a function : X X is one-one (respectively onto) if and only if is onto (respectively one-one). This is the characteristics property of a finite set. This is not true for infinite set.
A binary function * on A is a function * from A x A to A.
An element is the identity element for binary operation * : , if
An element is invertibel for binary operation * : if there exists such that where is the binary identity for the binary operation *. The element is called the inverse of and is denoted by .
An operation * on X is commutative, if in X.
functions class 12 unacademy,functions class 12 vedantu,functions class 12 maths,functions class 12 cbse,functions class 12 ncert,functions class 12 jee advanced,functions class 12 khan academy,functions class 12 boards,functions class 12 etoos,range class 12,functions class 12 for jee,domain class 12,types of mapping class 12,graphs of function,composition of a function,periodic function,inverse of a function,even odd function
If f(x) = log((1+x)/(1-x)), then f(2x/(1+x^2 )) is equal to
a)〖{f(x)}〗^2 b) 〖{f(x)}〗^3 c) 2f(x) d) 3f(x)
Relations and Functions For Class 12 Concepts
The topics and subtopics covered in relations and Functions for class 12 are:
Introduction
Types of relations
Types of Functions
Composition of functions and invertible functions
Binary operation.
Let us discuss the concept of relation and function in detail
Relation
The concept of relation is used in relating two objects or quantities with each other. If two sets are considered, the relation between them will be established if there is a connection between the elements of two or more non-empty sets.
Types of Relations
A relation in set A is a subset of A × A. Thus, A × A is two extreme relations.
Empty Relation
If no element of A is related to any element of A, i.e. R = φ ⊂ A ×A, then the relation in a set is called empty relation.
Universal Relation
If each element of A is related to every element of A, i.e. R = A × A, then the relation is said to be universal relation.
A relation R in a set A is called-
Reflexive- if (a,a) ∈ R, for every a ∈ A.
Symmetric- if (a1,a2) ∈ R implies that (a2,a1) ∈ R , for all a1,a2∈ A.
Transitive- if (a1,a2) ∈ R and (a2,a3) ∈ R implies that (a1,a3) ∈ R for all a1,a2,a3 ∈ A.
Equivalence Relation- A relation in a set A is equivalence relation if R is reflexive, symmetric and transitive.
Functions
A function is a relationship which explains that there should be only one output for each input. It is a special kind of relation(a set of ordered pairs) which obeys a rule i.e every X-value should be connected to only one y-value.
Types of Functions
One to one Function: A function f : X → Y is defined to be one-one (or injective), if the images of distinct elements of X under f are distinct, i.e., for every x1 , x2 ∈ X, f(x1 ) = f(x2 ) implies x1 = x2 . Otherwise, f is called many-one.
Onto Function: A function f : X → Y is said to be onto (or surjective), if every element of Y is the image of some element of X under f, i.e., for every y ∈ Y, there exists an element x in X such that f(x) = y.
One-one Function: A function f : X → Y is said to be one-one and onto (or bijective), if f is both one-one and onto.
Composition of Functions and Invertible Function
Let f : A → B and g : B → C be two functions. Then the composition of f and g, denoted by gof, is defined as the function gof : A → C given by;
gof (x) = g(f (x)), ∀ x ∈ A
Binary Operations
A binary operation ∗ on a set A is a function ∗ : A × A → A. We denote ∗ (a, b) by a ∗ b.
Example: Show that subtraction and division are not binary operations on R.
Solution: R × R → R, given by (a, b) → a – b, is not binary operation, as the image of (3, 5) under ‘–’ is 3 – 5 = – 2 ∉ R.
Similarly, ÷: R × R → R, given by (a, b) → a ÷ b is not a binary operation, as the image of (3, 5) under ÷ is 3 ÷ 5 = 3 5 ∉ R.
A function : X Y is one-one (or injective), if .
A function : X Y is onto (or surjective), if such that
A function : X Y is one-one-onto (or bijective), if is both one-one and onto.
The composition of function : A B and : B C is the function given by
A function : X Y is invertible, if such that and
A function : X Y is invertible, if and only if is one-one and onto.
Given a finite set X, a function : X X is one-one (respectively onto) if and only if is onto (respectively one-one). This is the characteristics property of a finite set. This is not true for infinite set.
A binary function * on A is a function * from A x A to A.
An element is the identity element for binary operation * : , if
An element is invertibel for binary operation * : if there exists such that where is the binary identity for the binary operation *. The element is called the inverse of and is denoted by .
An operation * on X is commutative, if in X.
functions class 12 unacademy,functions class 12 vedantu,functions class 12 maths,functions class 12 cbse,functions class 12 ncert,functions class 12 jee advanced,functions class 12 khan academy,functions class 12 boards,functions class 12 etoos,range class 12,functions class 12 for jee,domain class 12,types of mapping class 12,graphs of function,composition of a function,periodic function,inverse of a function,even odd function
 0:00:07
0:00:07
 0:07:48
0:07:48
 0:03:48
0:03:48
 0:03:01
0:03:01
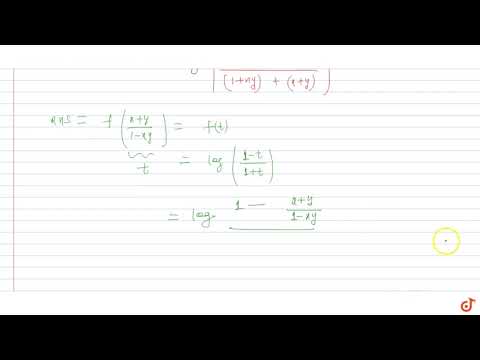 0:06:24
0:06:24
 0:08:00
0:08:00
 0:01:51
0:01:51
 0:01:16
0:01:16
 2:00:56
2:00:56
 0:01:56
0:01:56
 0:06:10
0:06:10
 0:04:57
0:04:57
 0:03:03
0:03:03
 0:02:01
0:02:01
 0:01:48
0:01:48
 0:02:30
0:02:30
 0:02:15
0:02:15
 0:05:12
0:05:12
 0:05:15
0:05:15
 0:03:10
0:03:10
 0:02:25
0:02:25
 0:03:47
0:03:47
 0:00:11
0:00:11
 0:00:43
0:00:43