Integral of tan^-1(1/(x^2-x+1)) from 0 to 1

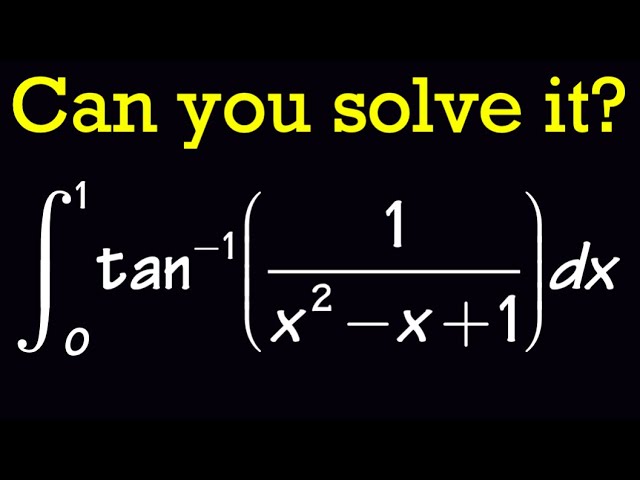
Показать описание

integral of arctan(1/(x^2-x+1)) from 0 to 1, integrate with inverse trig identities,

Please subscribe for more math content!

Рекомендации по теме

Комментарии

Calculus teachers HATE him. Learn how to integrate this with ONE WEIRD TRICK.

MrEnderChop

I wish IIT coaching classes had teachers like you.... interested, smart and who don’t teach like a loudspeaker

parthb

You won't believe what happens next.

mrmeowtv

When I first did this, I completely forgot to check for the obvious, splitting into simpler arctans method. I went on to solve using u=x-1/2 substitution, then another substitution and integration by parts, finally getting a u squared over a biquadratic in u to solve. Usually, I'd go with partial fraction decomposition, but the biquadratic didn't have real roots, so I took a deep breath, and split into complex roots instead. Got two standard integrals, but then after putting the limits, I had two arctans of complex numbers, which I proceeded to solve. Then performing complex division 8 times (and finding the roots of complex numbers twice), I finally got my answer with another complex multiplication.

It was a lot of fun.

green

I am right now in grade 10 and by seeing BLACKPENREDPEN videos, I have learned a good amount of calculus. I am sure this would help me in future. Good job bro!!!

Idunnowhoiam

You know jee, I am jee aspirant thank u

AbhishekKumar-vsfm

It is one of the oldest problems of IIT JEE ever. This came in the paper as a question of 8 marks about 3 decades ago when the IIT JEE exam was of subjective nature. The method demonstrated is not a shortcut trick- it is the only sane way to do the question, and was asked precisely to check whether the students were able to recognize it or not. Questions from single variable calculus in the JEE paper nowadays are far more complex and rarely involve direct evaluation of integrals.

ananyoroy

without interpreting through the graph we can use the property
Integral a to b f(x)=integral a to b f(a+b-x) and can remove the negative sign in the second integral by inter changing the limit and can proceed.just my idea☺.
And thanks "my fav teacher " for doing such good videos

I am requesting u to upload videos on statistics and probability.and thank u once again

vk

WE love the 10min answer to this 1 question! only 99 more questions to go and 2hr 40min left!

Saki

must recommend you to all the raccoons and birds interested in becoming engineers

DestinyQx

Amazing! Especially the little trick to combine the two different integrals into 2 times the same integral by showing that the second integral, the area "under" the curve from 0 to 1 was exactly the same as the negative integral/area of the first integral from 0 to 1. I would NEVER have come up with that simplification. Brilliant.

OCinTexile

I have so many memories with this exact same question. this makes me nostalgic and I miss school calc which we hated like just 10 months ago

akshat

Me gusta este video ... lo he visto varias veces. Me sorprende tu capacidad y lo lejos que has llegado bro!!

comingshoon

solve some integral problems releated to greatest integer function . frequently asked in jee mains.

anikbhowmick

Literally did this, then took a break to visit YouTube, and here it is.

green

Especially i started watching ur videos because i liked the way u teach with those different colours and the mic which u use is really different 😀

vk

I wish you would do more measure theoretic integral's...way more Fun !

vet_x

Nagyszerű példa, jól érthető megoldás.

prollysine

Great job...I've been looking for your videos for quite a while, I realized how important is to combine things together and being creative :-) this integral has been the hardest for me...so far, but I will discover others in your channel with pleasure :-) cheers

uzdefrederic

To come up with something this crazy one needs to have years of experience, and that's what students don't have. After Introducing to calculus if someone throws something like this, then that's it.
Just keep practicing. Your videos helped me to come up with new method to solve such problems. Your videos are helping me not just to think outside the box but what to think outside the box or which way I should take...
Thanks for the good work 🙂

md.iftakhar

Integral of tan^-1(1/(x^2-x+1)) from 0 to 1

Integral of tan^-1(1/(x^2-x+1)) from 0 to 1

Integral of tan^-1(x)/(1+x^2) - Integral example

What is `int_(0)^(1) (tan^(-1))/(1+x^(2))` dx equal to ?

Integral - Integrate Inverse Tan

Integral of tan^-1(x)

Evaluate the integral from limit 0 to 1 tan^-1 x/1+x^2 dx

If y = tan⁻¹(x), Prove that (1 + x²) d²y/dx² + (2x - 1) dy/dx = 0

If tan⁻¹(2x / 1-x²) + cot⁻¹(1 - x²/ 2x) = π/3 , Find x

Multivariate Calculus Tutorial 6 - Parametrization and Line Integrals

Evaluate : `int_(0)^(1)((tan^(-1)x)^(2))/(1+x^(2))dx`

Prove that the derivative of tan^(-1) x = 1/(1+ x^2). Derivatives of Inverse Trig Functions

Solve the equation tan⁻¹ ((1 - x)/(1 + x)) = 1/2 tan-1 x , (x greater than 0)

Integral of tan^-1 (2x/1-x²)

Integral of 1/(1+x^2)

Evaluating Inverse Trigonometric Functions

Evaluate: `int_(0)^(1)x^(2)tan^(-1)xdx`

Integration by Parts tan ^(-1) 1/x dx over [0, sqrt(3)] example 18. LIATE. Evaluate

How REAL Men Integrate Functions

Evaluate integral 0 to infinity tan^-1 x /x(1+x^2) dx | Integration of tan inverse x /x(1+x²)

Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school

Integrate 0 to 1 tan ^-1x dx

How to calculate inverse tan in scientific calculator #scintific #calculator #studenthacks

tan^-1 x / (1 + x^2) dx, Evaluate the indefinite integral.

Differentiate tan⁻¹(2x) / (1 + 15 x²)