filmov
tv
Linear Algebra: Lecture 37: nilpotent proofs, diagrammatics for generalize evectors, A = D + N
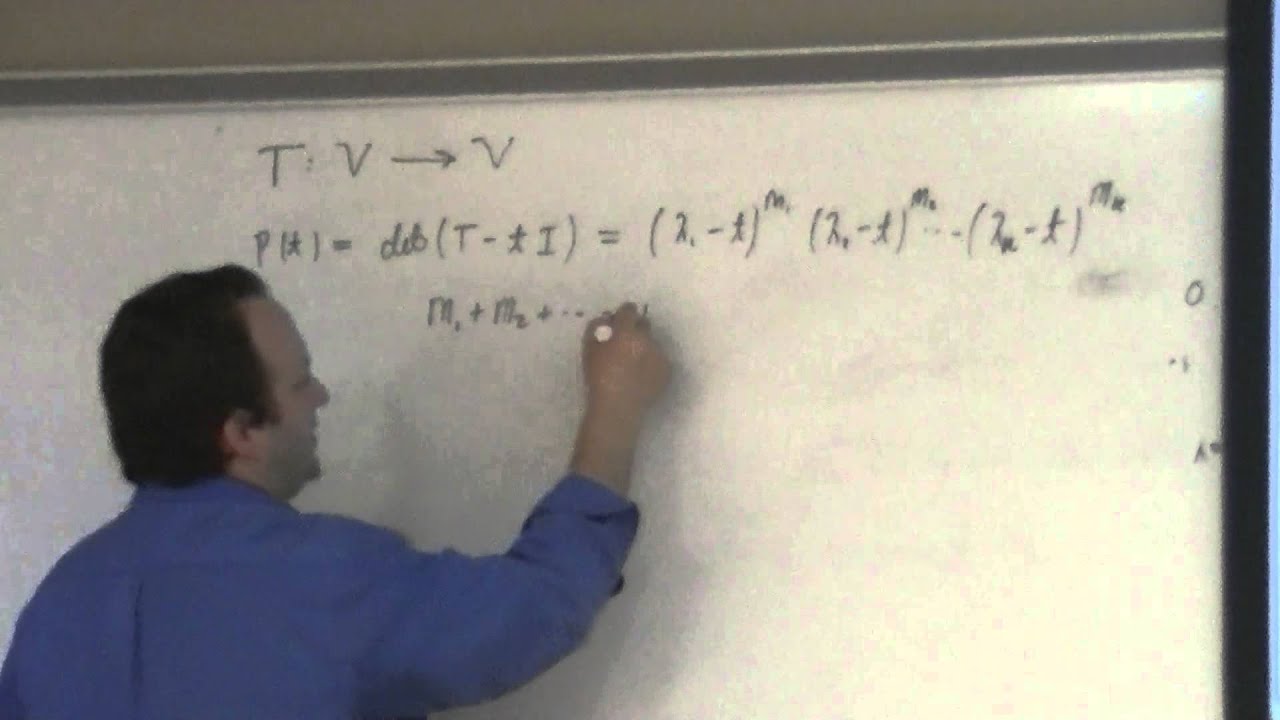
Показать описание
I yet again go through the set-up for the nilpotent map's cannonical form as built from the k-cycles. We also used the tableau to organize our thinking about the all the cycles for a given nilpotent map. This then is used to see where the Jordan blocks come from. Each Jordan block stems from looking at T-lambda*I restricted to K_i the i-th generalized e-space. I called this restricted map N_i and as it is nilpotent we are able to find a basis for K_i which places N_i in cannonical form. This leads to the Jordan form. I do not prove the central result, I encourage those interested to see the text for proof. Finally, I mention three major applications of the Jordan form. These are just the tip of the iceberg, next time: minimal polynomials and homework help.
 0:49:11
0:49:11
 1:37:27
1:37:27
 0:52:59
0:52:59
 0:29:23
0:29:23
 0:01:21
0:01:21
 0:52:16
0:52:16
 0:12:11
0:12:11
 0:12:13
0:12:13
 0:30:05
0:30:05
 0:01:16
0:01:16
 0:12:33
0:12:33
 0:13:04
0:13:04
 0:12:42
0:12:42
 0:04:21
0:04:21
 0:06:47
0:06:47
 0:01:23
0:01:23
 0:00:48
0:00:48
 0:20:37
0:20:37
 0:47:51
0:47:51
 0:19:05
0:19:05
 0:02:39
0:02:39
 0:02:34
0:02:34
 0:07:37
0:07:37
 0:05:16
0:05:16