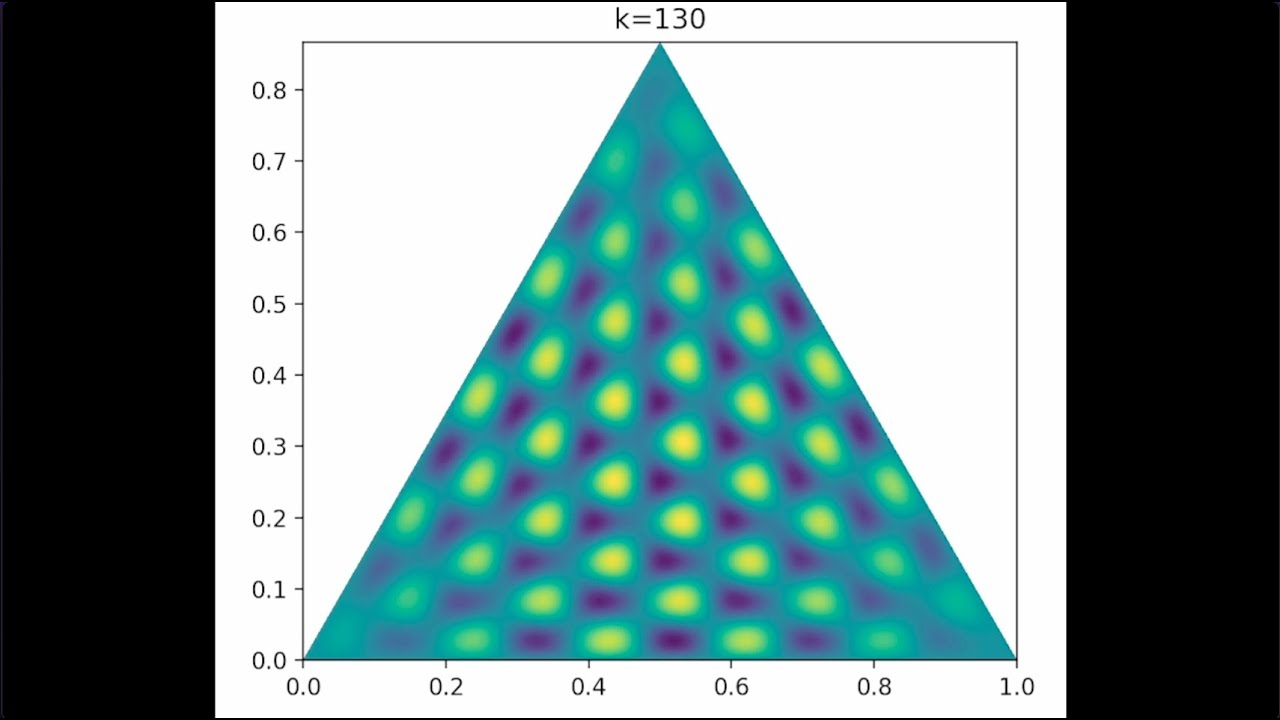
[-Δu=λu] The first 130 eigenfunctions of the Dirichlet Laplacian over a regular triangle

Mathematically simple entities create beautiful patterns like a kaleidoscope.

The first 130 Dirichlet Laplacian eigenfunctions over a regular triangle refer to a specific set of mathematical functions that arise when studying partial differential equations (PDEs) in the context of a regular triangular domain. To fully understand this concept, let's break it down into its components:

- the Laplace Operator: In mathematics, the Laplace operator (denoted by Δ) is a second-order differential operator that plays a crucial role in PDEs, particularly in physics and engineering problems. It is the sum of the second-order partial derivatives with respect to each of the coordinates, and it measures how a function's values change in relation to the average of the neighboring points.

- Dirichlet Boundary Conditions: Dirichlet boundary conditions specify the values of a function along the boundary of the domain. In the context of a regular triangle, this means specifying the function values on the three sides of the triangle.

- Eigenfunctions and Eigenvalues: When studying PDEs, eigenfunctions and eigenvalues are essential concepts. An eigenfunction is a non-zero function that, when acted upon by an operator (like the Laplacian), returns a scalar multiple of itself. This scalar multiple is known as the eigenvalue. Eigenfunctions and eigenvalues can be used to describe the behavior of a system and are essential in solving PDEs.

- When we talk about the "first 130 Dirichlet Laplacian eigenfunctions over a regular triangle," we are referring to the first 130 eigenfunctions that satisfy the Laplacian eigenvalue problem and the Dirichlet boundary conditions on a regular triangle domain. These eigenfunctions can be used to solve PDEs that model various phenomena, such as heat conduction, wave propagation, or fluid flow, within the triangular domain.

Computing these eigenfunctions involves solving the Laplacian eigenvalue problem subject to the Dirichlet boundary conditions. This can be a challenging task, but there are numerical and analytical methods available to calculate these eigenfunctions, such as the finite element method, the finite difference method, or the separation of variables technique.