filmov
tv
O que é Álgebra (II)

Показать описание
Continuarei a conversa sobre estruturas algébricas e seu papel dentro da Matemática.
Want to PASS Algebra 2? You better understand this…..
Learn Algebra 2
Algebra 2 in one minute!! #Algebra #Shorts
Learn Algebra 1 and 2 in One Video
ÁLGEBRA desde cero. Lo más importante y básico resumido en una clase
Logarithms | Logarithms | Algebra II | Khan Academy
Algebra 2 Midterm Exam Review
Solving Quadratic Equations Using The Quadratic Formula & By Factoring - Algebra 2
Maths Mairathan(Part-2) Bihar DElED Entrance Exam 💥 Previous Year Question 🎯Pcs Darpan
Algebra 2 – Base e and Natural Logs
Algebra 2 Final Exam Review
Simplifying rational expressions introduction | Algebra II | Khan Academy
Introduction to complex numbers | Imaginary and complex numbers | Algebra II | Khan Academy
What is a function? | Functions and their graphs | Algebra II | Khan Academy
Focus and directrix introduction | Conic sections | Algebra II | Khan Academy
Solving a quadratic equation by factoring | Algebra II | Khan Academy
Solving quadratic equations by completing the square | Algebra II | Khan Academy
Logarithmic Form to Exponential Form 🤯 #Shorts #algebra #math #maths #mathematics #education #learn...
Algebra Basics: Solving 2-Step Equations - Math Antics
Solving rational equations 2 | Polynomial and rational functions | Algebra II | Khan Academy
How to Multiply Radicals! 📚 #Shorts #algebra #math #maths #mathematics
Exponential Form to Logarithmic Form #Shorts #algebra #math #maths #mathematics #lesson #howto
Algebra 2: Chapter 2 Review 2018
Logarithmic Form to Exponential Form (Natural Log Edition) 🤯 #Shorts #algebra #math #education
Комментарии
 0:14:47
0:14:47
 0:16:04
0:16:04
 0:01:00
0:01:00
 2:52:42
2:52:42
 1:23:11
1:23:11
 0:07:02
0:07:02
 1:24:19
1:24:19
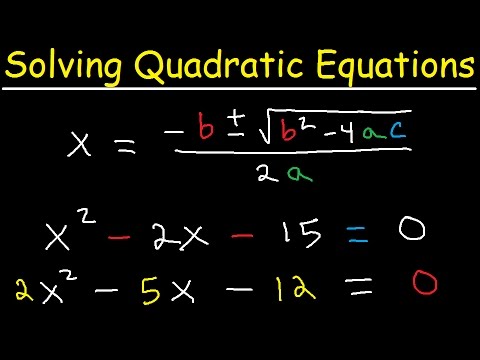 0:11:11
0:11:11
 2:29:50
2:29:50
 0:06:40
0:06:40
 1:37:17
1:37:17
 0:07:28
0:07:28
 0:04:39
0:04:39
 0:07:57
0:07:57
 0:04:06
0:04:06
 0:06:22
0:06:22
 0:14:06
0:14:06
 0:00:14
0:00:14
 0:10:29
0:10:29
 0:04:08
0:04:08
 0:00:22
0:00:22
 0:00:22
0:00:22
 0:20:41
0:20:41
 0:00:28
0:00:28