filmov
tv
Orthogonal, Involutory, Idempotent, Nilpotent and Periodic Matrices part-8

Показать описание
Orthogonal Matrix- A square matrix with real numbers or elements is said to be an orthogonal matrix, if its transpose is equal to its inverse matrix. Or we can say, when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an orthogonal matrix.
Involutory Matrix- In mathematics, an involutory matrix is a square matrix that is its own inverse. That is, multiplication by the matrix A is an involution if and only if A² = I, where I is the n × n identity matrix. Involutory matrices are all square roots of the identity matrix.
Idempotent Matrix-an idempotent matrix is a matrix which, when multiplied by itself, yields itself. That is, the matrix is idempotent if and only if . For this product to be defined, must necessarily be a square matrix.
A square matrix A such that An+1 = A is called a periodic matrix.
The minimum positive integer n with such property is called the period of the matrix A.
The following properties are direct from the definition:
(1) If A is nonsingular n - periodic matrix, then An = I.
(2) If A is nxn circulant matrix, then A is n - periodic matrix.
(3)The companion matrix of the polynomial p(x) = xn+1 - x is periodic matrix of period n.
(4) If A is nonsingular n - periodic matrix, then A⁻¹ is nonsingular
n -periodic matrix.
Involutory Matrix- In mathematics, an involutory matrix is a square matrix that is its own inverse. That is, multiplication by the matrix A is an involution if and only if A² = I, where I is the n × n identity matrix. Involutory matrices are all square roots of the identity matrix.
Idempotent Matrix-an idempotent matrix is a matrix which, when multiplied by itself, yields itself. That is, the matrix is idempotent if and only if . For this product to be defined, must necessarily be a square matrix.
A square matrix A such that An+1 = A is called a periodic matrix.
The minimum positive integer n with such property is called the period of the matrix A.
The following properties are direct from the definition:
(1) If A is nonsingular n - periodic matrix, then An = I.
(2) If A is nxn circulant matrix, then A is n - periodic matrix.
(3)The companion matrix of the polynomial p(x) = xn+1 - x is periodic matrix of period n.
(4) If A is nonsingular n - periodic matrix, then A⁻¹ is nonsingular
n -periodic matrix.
Комментарии
 0:05:08
0:05:08
 0:00:32
0:00:32
 0:02:50
0:02:50
 0:27:17
0:27:17
 0:22:14
0:22:14
 0:05:48
0:05:48
 0:02:18
0:02:18
 0:12:03
0:12:03
 0:20:01
0:20:01
 0:10:43
0:10:43
 0:00:20
0:00:20
 0:00:57
0:00:57
 0:08:22
0:08:22
 0:15:13
0:15:13
 0:17:30
0:17:30
 0:06:55
0:06:55
 0:00:16
0:00:16
 0:09:01
0:09:01
 0:44:26
0:44:26
 0:13:58
0:13:58
 0:13:42
0:13:42
 0:07:00
0:07:00
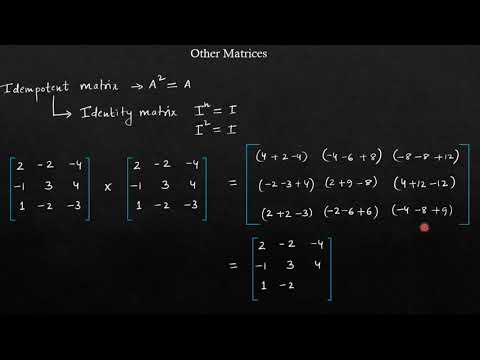 0:09:17
0:09:17
 0:10:08
0:10:08