filmov
tv
The Chaos Game: Different Rulesets

Показать описание
The so-called chaos game [1, 2] refers to a type of iterated map that can be used to approximate fractal patterns. In the video four popular examples, i.e. the Sierpiński carpet and hexagon as well as the fractal starfish and the fractal fern, are given. In general, the iterative procedure can be written as a set of affine transformations. From this set of transformations (ruleset) a specific one is chosen (per iteration) at random. Given a suitable ruleset, the resulting set of points lies dense in a fractal set.
[1] R. L. Devaney, Chaos Rules!, Math Horizons 12(2), 11 (2004).
[1] R. L. Devaney, Chaos Rules!, Math Horizons 12(2), 11 (2004).
The Chaos Game: Different Rulesets
Sierpiński Gasket: The Chaos Game (100 Million Samples)
The Chaos Game
The Chaos Game in Pentagon, Octagon, and Square (math visualization)
Impound Chaos Trading Card Game (Rules & Gameplay)
NO RULES ⛔️ NO CONTROL 🚫 JUST CHAOS 🙈 How Do I Escape?! 😰 Sprunki Pinki Part 2 #shorts #minecraft...
Average Game Vs Chaos Legionary #40k #killteam40k
Dicast: Rules of Chaos - A Few Tips for Beginners (What to play first turn!)
Lookin' For Games Weekly Update: LFG: Chaos Rules!
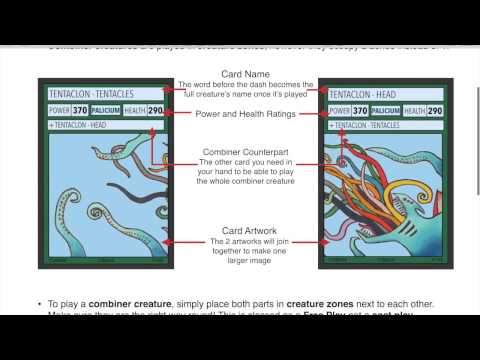
Chaos Galaxy TCG Official Rules - Part 1/2
DICAST: RULES OF CHAOS - First Impressions
Warhammer 40k Meme Dub: Haarken Worldclaimer Meets The New Chaos Lord With Jump Pack
[ Custom ] takehirotei - Rules of the Chaos Dilemma
Chaos Galaxy TCG Rules: How to play the game Part 1(v2.0)
Chaos Rules 🌑⚫#venom #shortvideo #shorts #short #godzilla #anime #batman #live #kaiju #warhammer40k...
Why rules are important?
Misha never disappoint whether in Moc,Apoc,PF 🔥
They Made Ice Cream With Their Bare Hands?! | Squid Game Slime ASMR Scoop!
New Obliterators rules | Chaos Space Marines Warhammer 40k 10th Edition
Chaos Galaxy TCG Official Rules - part 2/2
Minecraft Movie Chicken Jockey Movie Theater Chaos😱
Some experiments with chaos game.
The Chaos of Medieval Football
Wierdest ipl rules ever !!🤯
Комментарии
 0:02:15
0:02:15
 0:01:16
0:01:16
 0:01:36
0:01:36
 0:02:03
0:02:03
 0:05:17
0:05:17
 0:00:05
0:00:05
 0:00:51
0:00:51
 0:02:20
0:02:20
 0:08:41
0:08:41
 0:16:07
0:16:07
 0:14:15
0:14:15
 0:00:55
0:00:55
![[ Custom ]](https://i.ytimg.com/vi/HLZ9vuWjpgs/hqdefault.jpg) 0:06:03
0:06:03
 0:10:00
0:10:00
 0:00:06
0:00:06
 0:05:42
0:05:42
 0:00:34
0:00:34
 0:00:13
0:00:13
 0:00:07
0:00:07
 0:22:46
0:22:46
 0:00:25
0:00:25
 0:01:19
0:01:19
 0:00:28
0:00:28
 0:00:59
0:00:59