The function f is defined by f(x) = ax^2 + bx + c, where a, b, and c are constants. The graph of...

Показать описание

Bluebook Digital SAT Practice Test 6, Section 2, Module 2 (HARD), Question 22:

The function f is defined by f(x) = ax^2 + bx + c, where a, b, and c are constants. The graph of y = f(x) in the xy-plane passes through the points (7, 0) and (-3, 0). If a is an integer greater than 1, which of the following could be the value of a + b?

KEEP IN TOUCH:

Рекомендации по теме

Комментарии

Thanks, this method is way better than previous one. I am taking SAT on 24th August, do you have any recomendation, please?

Mr_Assierne

Thanks a lot! I’ve been watching your videos non stop for the past week and they are all insanely helpful!

ladaal

We can also use the vertex form.
a (x - 2)^2 + k
ax^2 - 4ax + 4a + k
Thus,
a+b = -3a
Just like in the video

Thus, all we need to show is that the “c” terms are the same.
c = - 21a (video)
c = 4a + k (here)
Is k equal to - 25a ?

Let’s put the equation in the video into the vertex form.
a (x - 2)^2 - 21a - 4a
K is indeed equal to - 25a

OverclockingCowboy

Could you explain the first part of the solution please? f(x) = a (x-7) (x+3) = 0

yeet

why do we eliminate the choice c and d? although a>1 it doesn't mean a+b is also greater than 1 isn;t?

suachoi

i dont understand the last part like the a-4a part and so forth

onedoorhrshy

how do you know it equals -3a when you have a-4a

youngstratus

Does come under algebra or advance maths

GeetaAkshara

The function f is defined by f(x) = ax^2 + bx + c, where a, b, and c are constants. The graph of...

The function f is defined by f(x) = ax + b, where an and b are constants. In the xy-plane, the.....

The function f is defined by f(x) = 9x - 16. What is the value of f(3)?

The function f is defined by f(x) = ax^2 + bx + c, where a, b, and c are constants. The graph of...

Function f is defined by f(x) = (x + 6) (x + 5) (x + 1). Function g is defined by g(x) = f(x - 1)...

The function f is defined by f(x) = 8x. For whatvalue of x does f(x) = 72 ?

For x is greater than 0, the function f is defined as follows: f(x) equals 201% of x. Which of....

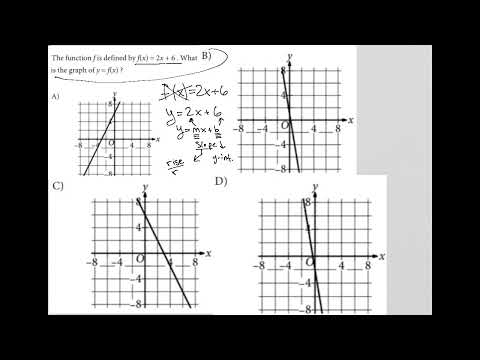
The function f is defined by f(x) = 2x + 6. What is the graph of y = f(x)?

f(x) = (1.84)^x/4; The function f is defined by the given equation. The equation can be rewritten...

in Composite Functions and Inverses Explained: Questions and Conditions

The function f is defined by f(x) = (-8) (2)^x + 22. What is the y-intercept of the graph of y...

The function f is defined by f(x) = ax^2 + bx + 6, where a, b, and c are constants. The graph of....

The function f is defined by f(x) = 8sqrt(x). For what value of x does f(x) = 48 ?

The function f is defined by f(x) = 1/10 x - 2. Whatis the y-intercept of the graph of y = f(x)...

The function f is defined by f(x) = (x+15)/5, and f(a) = 10, where a is a constant. What is the.....

The function f is defined by f(x) = (x - 6)(x - 2)(x + 6). In the xy-plane, the graph of y = g(x)...

The function f is defined by f(x) = (x - 6) (x - 2)(x + 6). In the xy-plane, the graph of y = g(x)..

The function f is defined by f(x) = a sqrt(x + b), where an and b are constants. In the xy-plane....

The function f is defined by f(x) = (x+3)(x+1). The graph of f in the xy-plane is a parabola....

The rational function f is defined by an equation in the form f(x) = a/x+b, where a and b are...

Function f is defined by f(x) =-a^x + b, where an and b are constants. In the xy-plane, the....

The function f is defined by a polynomial. Some values of x and f(x) are shown in the table above..

f(x) =9(4)^x; The function f is defined by the given equation. If g(x) = f(x + 2), which of the....

For x is greater than 0, the function f is defined as follows: f(x) equals 201% of x. Which of the..

The function f is defined by f(x)=(-8)(6)^x-4. What is the y-intercept of the graph of y=f(x) in...