filmov
tv
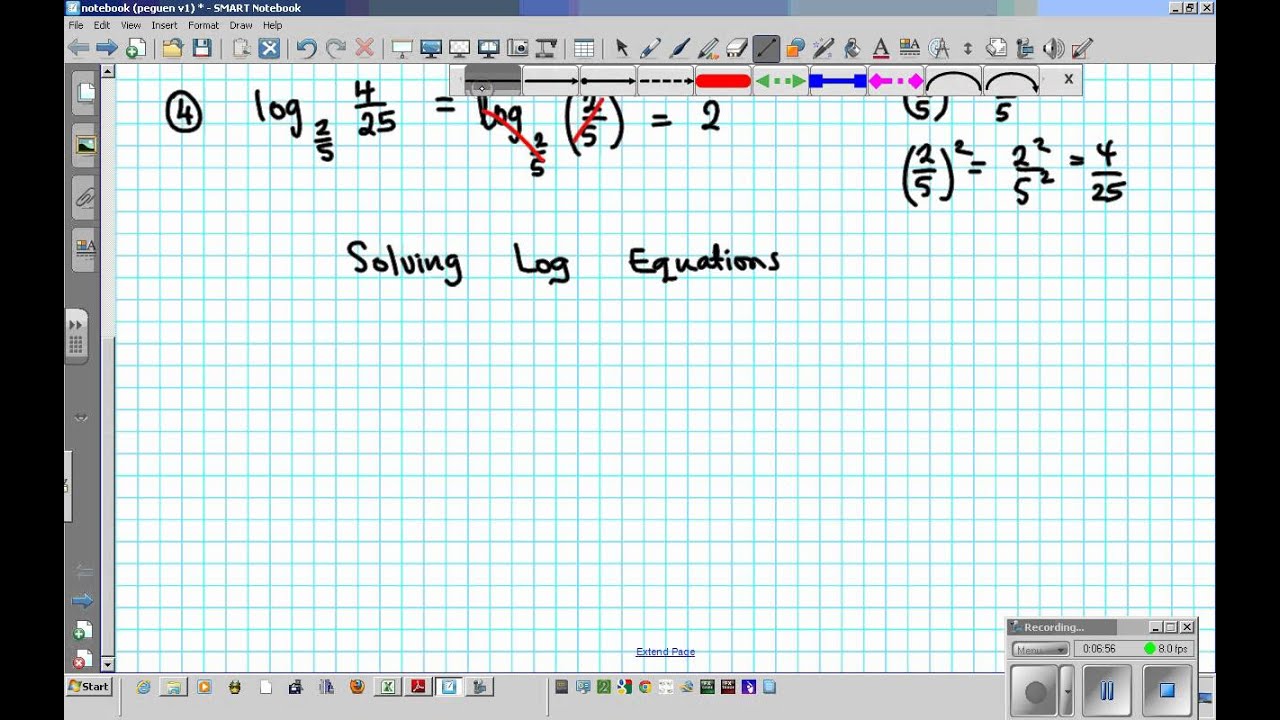
TU4L5 Simplifying logarithmic equations
Показать описание
Math Tutorials Links
Algebra
Foundations
Equations
Inequalities
Solve Systems of Equations by Graphing
TESTS
To expand logarithms, you can use the following rules:
1. Product rule: The product rule of logarithms states that log base b of (x * y) is equal to the sum of log base b of x and log base b of y. Therefore, to expand a logarithm of a product, you can split it into the sum of logarithms of each factor. For example:
log base 2 of (x * y) = log base 2 of x + log base 2 of y
2. Quotient rule: The quotient rule of logarithms states that log base b of (x / y) is equal to the difference of log base b of x and log base b of y. Therefore, to expand a logarithm of a quotient, you can split it into the difference of logarithms of the numerator and denominator. For example:
log base 2 of (x / y) = log base 2 of x - log base 2 of y
3. Power rule: The power rule of logarithms states that log base b of (x^y) is equal to y times log base b of x. Therefore, to expand a logarithm of a power, you can multiply the exponent by the logarithm of the base. For example:
log base 2 of (x^3) = 3 * log base 2 of x
4. Change of base formula: The change of base formula allows you to change the base of a logarithm. It states that log base b of x can be expressed as log base a of x divided by log base a of b. Therefore, to expand a logarithm with a different base, you can use the change of base formula to express it in terms of a logarithm with a known base. For example:
log base 2 of x = log base 10 of x / log base 10 of 2
It's important to remember that when expanding logarithms, you may need to simplify or combine terms afterwards to get the expression into a more useful or simplified form.
Algebra
Foundations
Equations
Inequalities
Solve Systems of Equations by Graphing
TESTS
To expand logarithms, you can use the following rules:
1. Product rule: The product rule of logarithms states that log base b of (x * y) is equal to the sum of log base b of x and log base b of y. Therefore, to expand a logarithm of a product, you can split it into the sum of logarithms of each factor. For example:
log base 2 of (x * y) = log base 2 of x + log base 2 of y
2. Quotient rule: The quotient rule of logarithms states that log base b of (x / y) is equal to the difference of log base b of x and log base b of y. Therefore, to expand a logarithm of a quotient, you can split it into the difference of logarithms of the numerator and denominator. For example:
log base 2 of (x / y) = log base 2 of x - log base 2 of y
3. Power rule: The power rule of logarithms states that log base b of (x^y) is equal to y times log base b of x. Therefore, to expand a logarithm of a power, you can multiply the exponent by the logarithm of the base. For example:
log base 2 of (x^3) = 3 * log base 2 of x
4. Change of base formula: The change of base formula allows you to change the base of a logarithm. It states that log base b of x can be expressed as log base a of x divided by log base a of b. Therefore, to expand a logarithm with a different base, you can use the change of base formula to express it in terms of a logarithm with a known base. For example:
log base 2 of x = log base 10 of x / log base 10 of 2
It's important to remember that when expanding logarithms, you may need to simplify or combine terms afterwards to get the expression into a more useful or simplified form.
 0:13:37
0:13:37
 0:06:03
0:06:03
 0:03:58
0:03:58