filmov
tv
0.bbbb... = 1 (in base b+1) | 9 geometric series dissection proofs without words

Показать описание
This is a compilation of nine shorts (most with words). If you want to see those, the links are below (along with attribution to the original ``proof without words" author).
00:38 Infinite sum of powers of 1/3 (0.222... = 1 in base 3):
01:20 Infinite sum of powers of 1/4 (0.333... = 1 in base 4):
01:55 Infinite sum of powers of 1/5 (0.444... = 1 in base 5):
02:40 Infinite sum of powers of 1/6 (0.555... = 1 in base 6):
03:20 Infinite sum of powers of 1/7 (0.666... = 1 in base 7):
04:15 Infinite sum of powers of 1/8 (0.777... = 1 in base 8):
05:00 Infinite sum of powers of 1/9 (0.888... = 1 in base 9):
05:50 Infinite sum of powers of 1/10 (0.999... = 1 in base 10):
To learn more about animating with manim, check out:
___________________________________
Music:
Creative Commons / Attribution 4.0 International (CC BY 4.0)
0.bbbb... = 1 (in base b+1) | 9 geometric series dissection proofs without words
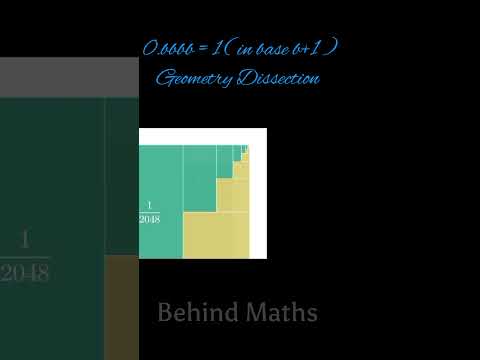
0.bbbb = 1 ( in base b+1 ) | Geometry Dissection #shorts #viral
Diana and Roma - mysterious challenge in the house
Cargador inalámbrico 3 en 1 (base de carga múltiple)! BBB!. CDC-1.60
Base Fluída Dapop #basebocarosa #catharinehills #makeup #viral #melu #bbb
Playtime at Playground | Playground Song +More Nursery Rhymes | Kids Songs | BabyBus
Bebé Juan, ¡No Más Dulces! 🍬🍭🍫 | Canciones Infantiles | Little Angel Español
Marçal rejeita apoio a Nunes e prevê vitória de Boulos em São Paulo | Giro VEJA
MT - NO PIQUE BBB (DJ 2L DE VILA VELHA) MC RODRIGO DO CN { Feat. MC CYCLOPE } - TERROR DO ES 027
#patrickstarrrgiveaway Turn Up the Base Blurring Foundation BBB CREAM for medium skin tones
VOCÊ PREFERE O GEORGE OU VOID??? #emillyvickof #katlenof #peppapig
One Size Beauty Turn Up The Base BBB cream foundation Review & Wear Test! #onesize #foundation
Sophia Grace and Rosie perform 'Super Bass' 11 years later #ellen #shorts
BASE OU BB CREAM? QUAL COMPRAR? - #Tutorial20
I turned my BEGINNER HOUSE into the BEST MODERN HOUSE in MINECRAFT!
Psi Patrol Polska | Piosenka Czołówkowa (Muzyka) | Nick Jr.
Base BBB do momento O Boticário R$21 🤩 #shorts #maquiagem
Bento e Totó - Água (Desenho Infantil)
VOCÊ PREFERE O GEORGE OU VOID??? #emillyvickof #katlenof #peppapig
#111 #base #bbb #learning #tricks #viralshorts
Nueva base para notebook Nisuta, triple BBB 👉Buena Bonita Barata👈NSCN6M🔥
FIZ um BBB com os BRAWLERS do BRAWL STARS!
*NEW* ONE/SIZE TURN UP THE BASE BBB CREAM OILY SKIN | #shorts #tiktok
NOVA ATUALIZAÇÃO no BROOKHAVEN! (novo banco secreto)
Комментарии
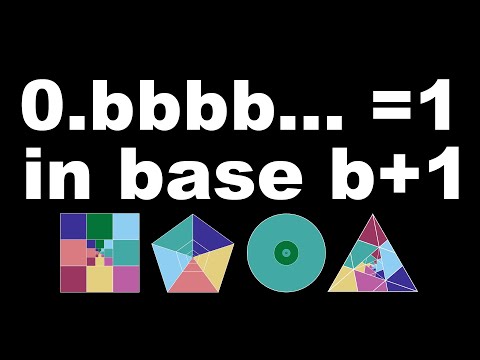 0:06:51
0:06:51
 0:00:32
0:00:32
 0:07:29
0:07:29
 0:07:36
0:07:36
 0:00:30
0:00:30
 0:21:32
0:21:32
 1:02:41
1:02:41
 0:01:49
0:01:49
 0:02:04
0:02:04
 0:00:06
0:00:06
 0:01:01
0:01:01
 0:00:17
0:00:17
 0:01:00
0:01:00
 0:08:15
0:08:15
 0:11:29
0:11:29
 0:00:40
0:00:40
 0:00:18
0:00:18
 0:01:58
0:01:58
 0:01:01
0:01:01
 0:00:15
0:00:15
 0:00:31
0:00:31
 0:30:28
0:30:28
 0:00:39
0:00:39
 0:09:10
0:09:10