filmov
tv
How to find number of turning points of polynomial using Formula from equations with 5 examples

Показать описание
CAUTION: The formula discussed for the number of turning points will not work when we have imaginary roots. It always works for Real roots. Thanks
How To Find Someone Location By Phone Number || 2025
Find number of triangles |Counting figures | RAILWAY , NTPC , MTS , SSC, CGL #reasoning #shorts
How to find Number of Triangles in a Figure 👍🤔
How to find Serial Number of iPhone | Serial Number iPhone | iPhone tips
How To Find Someone Location By Phone Number
The Easiest Way to Find Number of Triangle. #shorts
How to Find the Number of Protons, Neutrons and Electrons
Calculating Percentages | How to Find a Percent of a Number
🔥 find the odd number 93 🤯part no 102 🧐 math is easy #quiz #puzzle #riddles #shorts
Trick To Find Number Of Cubes | Counting Figures Trick | Maths tricks #shorts #maths #imransirmaths
Excel formula to find the number of working days between two Dates
How to find number of syllables in a word? | check pin comment
Find The Next Number In The Sequence | Math Problem
Find the number for NO CALLER ID!! #shorts
shortcut method to find square of any number #math #education
How to Find Your Own Phone Number on Android
Find the number of characters using LEN function in Excel
Relations and functions: how to find number of relation A to B #maths #cbse #education #ncert
how to find anyone number in snapchat#viral#shorts
How to find total number of factors || Number System concept || #youtubeshorts #shorts #maths
How to find a no caller ID number
How to find Factors of a number in 10 Seconds! #math #tutor #factors #factorsandmultiples
How to Find a Percent of a Number | Math with Mr. J
#Shorts Calculator Tricks | Find any Number of #Antilog
Комментарии
 0:00:33
0:00:33
 0:00:16
0:00:16
 0:00:16
0:00:16
 0:00:17
0:00:17
 0:01:50
0:01:50
 0:00:32
0:00:32
 0:00:39
0:00:39
 0:09:45
0:09:45
 0:00:05
0:00:05
 0:00:50
0:00:50
 0:00:35
0:00:35
 0:00:24
0:00:24
 0:00:25
0:00:25
 0:00:14
0:00:14
 0:00:15
0:00:15
 0:01:22
0:01:22
 0:00:30
0:00:30
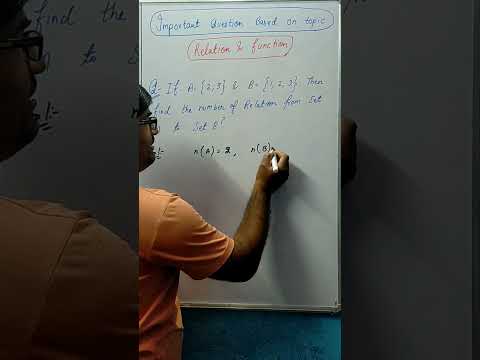 0:00:30
0:00:30
 0:00:17
0:00:17
 0:00:57
0:00:57
 0:00:15
0:00:15
 0:01:00
0:01:00
 0:04:56
0:04:56
 0:00:39
0:00:39