filmov
tv
But You Can't Do That

Показать описание
🙏Support me by becoming a channel member!
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information.
#math #brithemathguy #logarithm
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information.
#math #brithemathguy #logarithm
But You Can't Do That
Minecraft But You Can Never Die
Why you understand English but CAN'T speak FLUENTLY
Minecraft but you can NEVER find what you NEED
Minecraft But Jumping Gives You Random Items
Minecraft Skyblock, but EVERYTHING Is EMERALD LUCKY BLOCKS.
Minecraft, But You Only Get One Block!
Minecraft, But You Can Craft Structures...
When You Have 1000 Ideas But You Can't Choose One
Minecraft But Everything I Touch turns to VOID
Minecraft but you can Eat Biomes
Minecraft, But You Have An OVERPOWERED Pickaxe
Why You Can UNDERSTAND English But You STRUGGLE TO SPEAK In English
Hate Your Job But Don't Want To Quit? Try Quiet Quitting instead.
Dress To Impress But I Can't See The Theme
Five things you allegedly can't do in Germany (but you can)
Minecraft but there are Custom Hearts
Minecraft, But With Only Half a Heart
CEO Hate Ugly Wife&Flirts With Mistress! But When She Dumps Him And Shows Up Stunningly, He Regr...
How to Do Something That Should Be Easy (But...Is...Not)
HOW TO DO THE SECRET DRESS TO IMPRESS QUEST + NEW UPDATES SOON...
Minecraft, But You Shapeshift Every Minute...
When you are on Squid Games 2 but you watch too much anime
Why Can't I Understand Native English Speakers, But I Can Understand You?
Комментарии
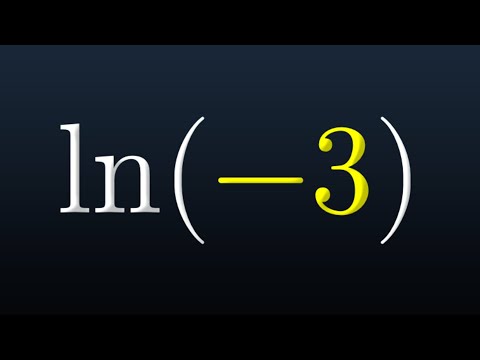 0:03:14
0:03:14
 0:13:32
0:13:32
 0:07:25
0:07:25
 0:04:44
0:04:44
 0:14:59
0:14:59
 0:18:22
0:18:22
 0:19:30
0:19:30
 0:17:27
0:17:27
 0:08:56
0:08:56
 0:10:24
0:10:24
 0:14:16
0:14:16
 0:18:45
0:18:45
 0:27:09
0:27:09
 0:11:13
0:11:13
 0:17:31
0:17:31
 0:04:41
0:04:41
 0:14:02
0:14:02
 0:17:09
0:17:09
 2:04:10
2:04:10
 0:06:42
0:06:42
 1:04:46
1:04:46
 0:19:09
0:19:09
 0:00:23
0:00:23
 0:10:20
0:10:20