filmov
tv
Why Does 0! = 1

Показать описание
►WEBSITE
►MY COURSE
Prove It Like A Mathematician! (Intro To Math Proofs)
►BECOME A CHANNEL MEMBER
#math #brithemathguy #shorts
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information. Viewers should always verify the information provided in this video by consulting other reliable sources.
►MY COURSE
Prove It Like A Mathematician! (Intro To Math Proofs)
►BECOME A CHANNEL MEMBER
#math #brithemathguy #shorts
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information. Viewers should always verify the information provided in this video by consulting other reliable sources.
Why is 0! = 1?
But Why Does 0 Factorial Equal 1
Why Does 0! = 1
Why Does 0! = 1
Why Does 0! = 1? | Combinatorics
But Why Does 0! = 1
Zero Factorial - Numberphile
Why does x to the power of 0 equal 1?
Why Any Number to the Power of 0 Equals 1 - Explained Simply in Bengali
But Why Does 0! = 1
Why Does 0! = 1
Why Do Computers Use 1s and 0s? Binary and Transistors Explained.
The Most Controversial Number in Math
Binary Explained in 01100100 Seconds
Why Does 0! = 1?
Does 1/0 = Infinity? #shorts
Why does 0! = 1?
Why does 0 factorial equals 1?
Why does 0! = 1?
Why can't you divide by zero? - TED-Ed
Why does 0! = 1? #maths #mathstips #basicmaths
Why does 'x to the zero power' equal 1?
Why Does 0! = 1? #shorts
Why Does 0! = 1?
Комментарии
 0:06:05
0:06:05
 0:04:49
0:04:49
 0:00:34
0:00:34
 0:00:23
0:00:23
 0:11:37
0:11:37
 0:00:15
0:00:15
 0:07:36
0:07:36
 0:00:46
0:00:46
 0:05:22
0:05:22
 0:00:31
0:00:31
 0:00:43
0:00:43
 0:07:00
0:07:00
 0:06:46
0:06:46
 0:02:27
0:02:27
 0:06:56
0:06:56
 0:00:57
0:00:57
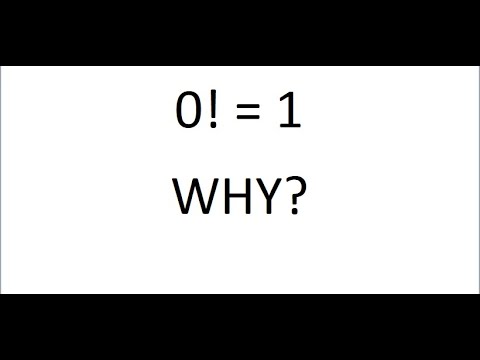 0:05:44
0:05:44
 0:02:03
0:02:03
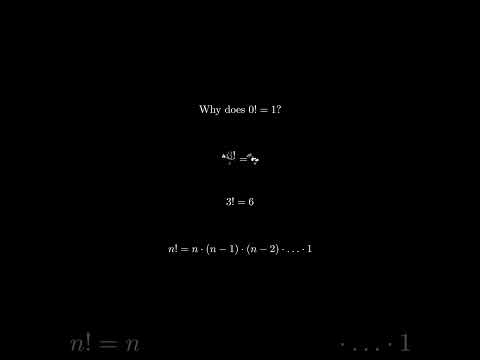 0:00:46
0:00:46
 0:04:51
0:04:51
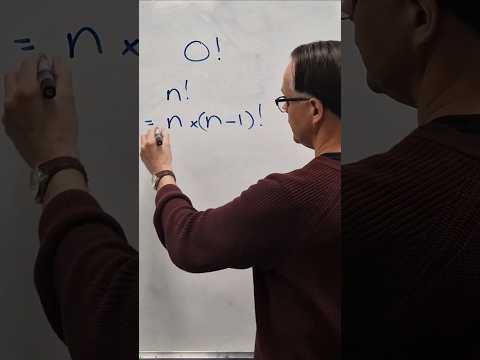 0:00:45
0:00:45
 0:02:15
0:02:15
 0:00:45
0:00:45
 0:00:43
0:00:43