filmov
tv
A few more proofs involving sets.
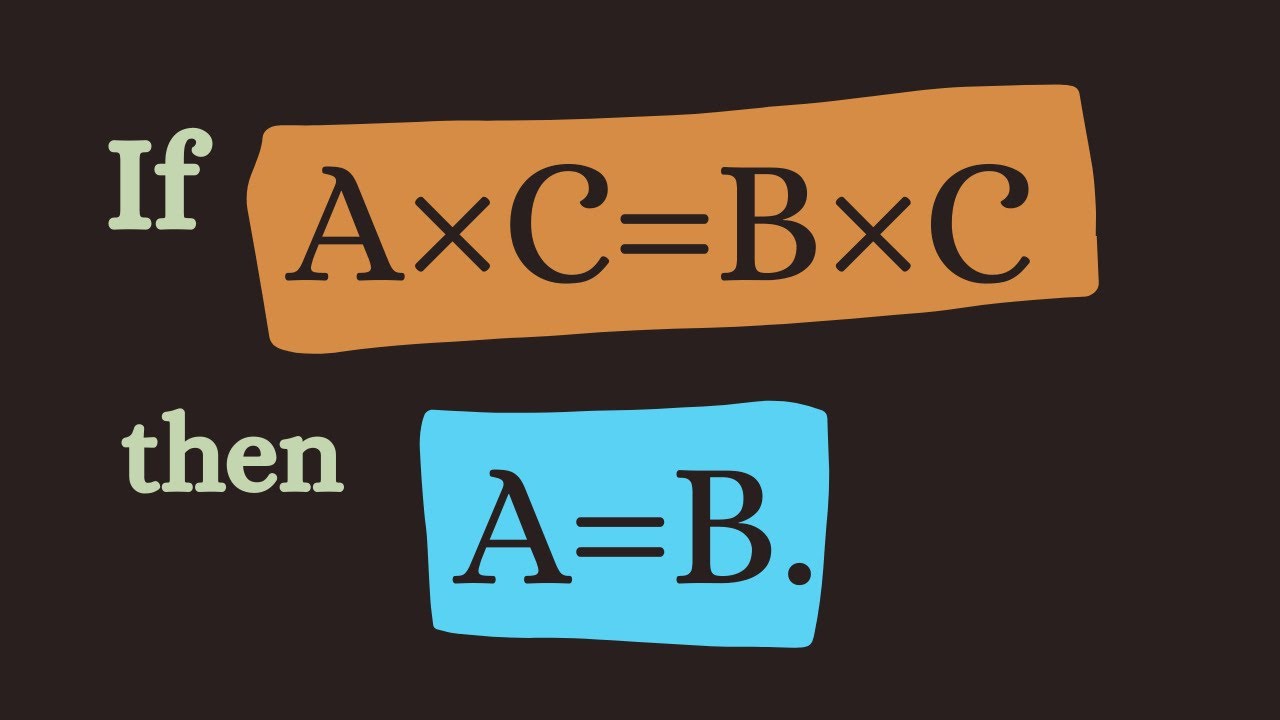
Показать описание
We look at a few more proofs involving sets.
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
A few more proofs involving sets.
Proving Sets
Proof and Problem Solving - Quantifiers Example 03
Geometry Proofs Explained! Triangle Congruence
Mathematical Induction Practice Problems
Basic proofs involving sets.
Discrete Math Proofs in 22 Minutes (5 Types, 9 Examples)
How to do a PROOF in SET THEORY - Discrete Mathematics
How to do a Geometry Proof – Step-by-Step Lesson
Proofs involving cases.
Ext 2: Proof (Proofs Involving Inequalities)
Proofs involving Inequalities
Everyone Proofs - More Two-Column Proofs on Segments | Geometry Help
More proofs of trig identities
Math Reasoning: Proofs involving sets II
2 1, part 4 Some proofs involving sets
Proof by Contradiction | Method & First Example
An Intro to Proof Based Math: Direct Proofs Involving the Congruence of Integers
Learn How To Prove A Trigonometry Question & Apply Trig Identities Effectively
Everyone Proofs - More Segment and Angle Two-Column Proofs | Geometry Hep
Algebraic Proofs (involving integers)
More Practice With Proofs Involving Least Upper Bounds | Introduction to Real Analysis
Geometric Proofs Involving Parallel Lines (Extra Practice Topic 8)
Direct Proofs Involving Divisibility
Комментарии
 0:09:40
0:09:40
 0:22:12
0:22:12
 0:06:35
0:06:35
 0:09:43
0:09:43
 0:18:08
0:18:08
 0:21:56
0:21:56
 0:22:09
0:22:09
 0:16:30
0:16:30
 0:27:05
0:27:05
 0:13:52
0:13:52
 0:10:18
0:10:18
 0:04:44
0:04:44
 0:37:11
0:37:11
 0:12:40
0:12:40
 0:20:08
0:20:08
 0:07:52
0:07:52
 0:09:00
0:09:00
 0:36:57
0:36:57
 0:13:17
0:13:17
 0:15:22
0:15:22
 0:17:02
0:17:02
 0:23:18
0:23:18
 0:15:19
0:15:19
 0:17:06
0:17:06